
现代游戏引擎 - 游戏引擎中物理系统的基础理论和算法(十)
物理系统
物理系统是游戏引擎的重要组成部分。 在游戏中玩家和整个游戏世界的互动都是依赖于物理系统的实现,同时在现代游戏中大量的粒子效果也都是通过物理系统来进行驱动的。
显然物理系统非常复杂,甚至于有很多公司专门去研究物理引擎的高效实现。 而在本课程中我们同样把物理系统拆分成两节,
这一节课主要介绍物理引擎的基本概念而在下一节课中则会更多地讨论游戏业界更前沿的物理仿真技术。
物理对象与形状
对象
- 静态对象:Static
- 动态对象:Dynamic
- Trigger:碰撞检测区域
- Kinematic对象:不符合物理原理,玩法逻辑控制
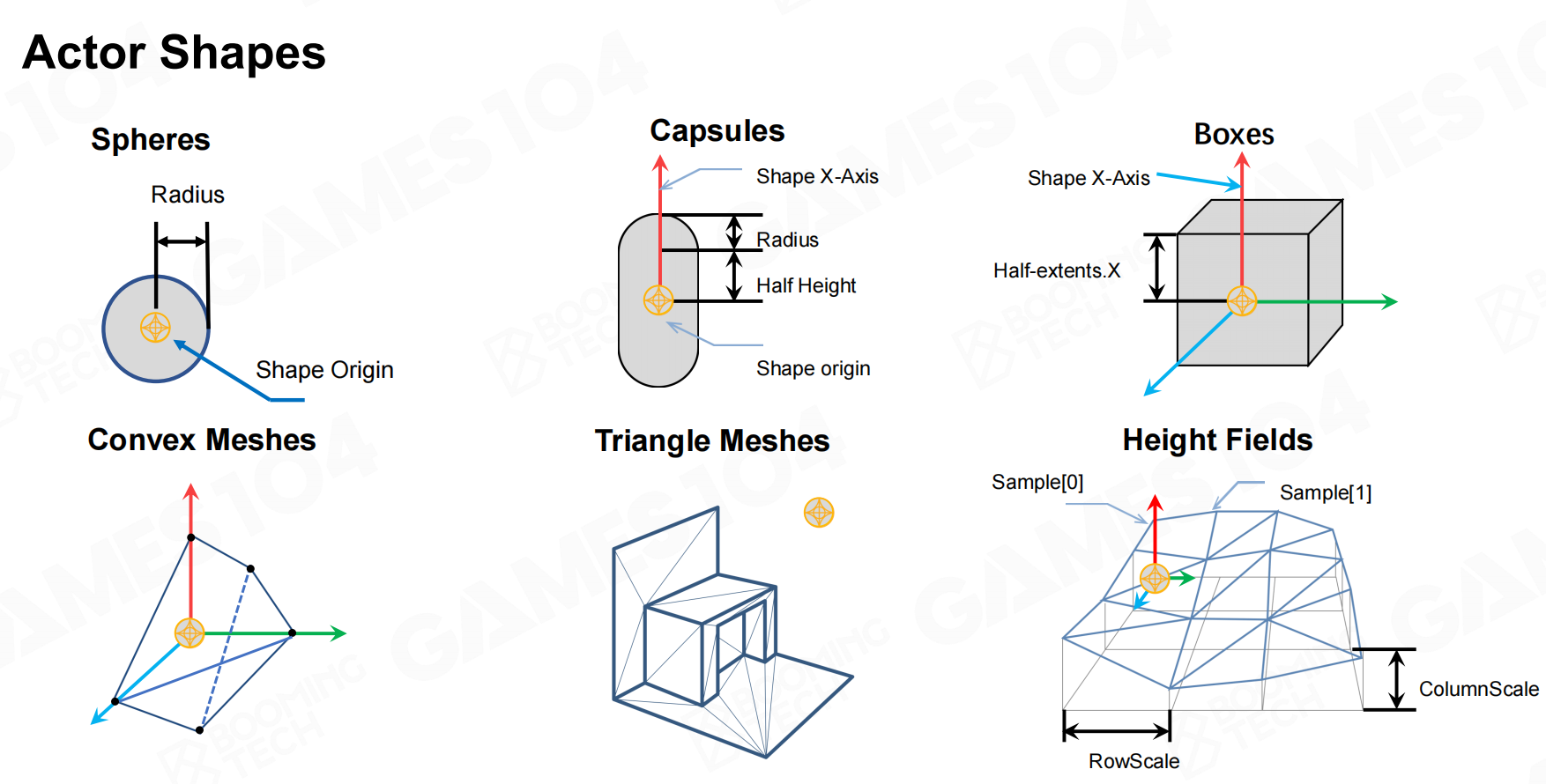
形状
- 球
- 胶囊体
- 立方体
- 凸多边形 Convex Meshes
- 三角面
- 高度图:多见于地形
当我们利用这些对象去组成实际需要的物体对象时,有两个原则:
- 形状接近就好,不一定要完美
- 简单性。要尽量用简单的对象去拼接(比如尽量少用三角网格),且越少越好。
用物理形状包裹对象
此外,一些比较重要的物理概念:
- 质量和密度 Mass and Density
- 质心(做载具时很重要)Center of Mass
- 摩擦和恢复(弹性) Friction & Restitution
力于运动
力
一般我们把力分成两种:
- Force 可以理解为直接的重力、拉力、摩擦力等
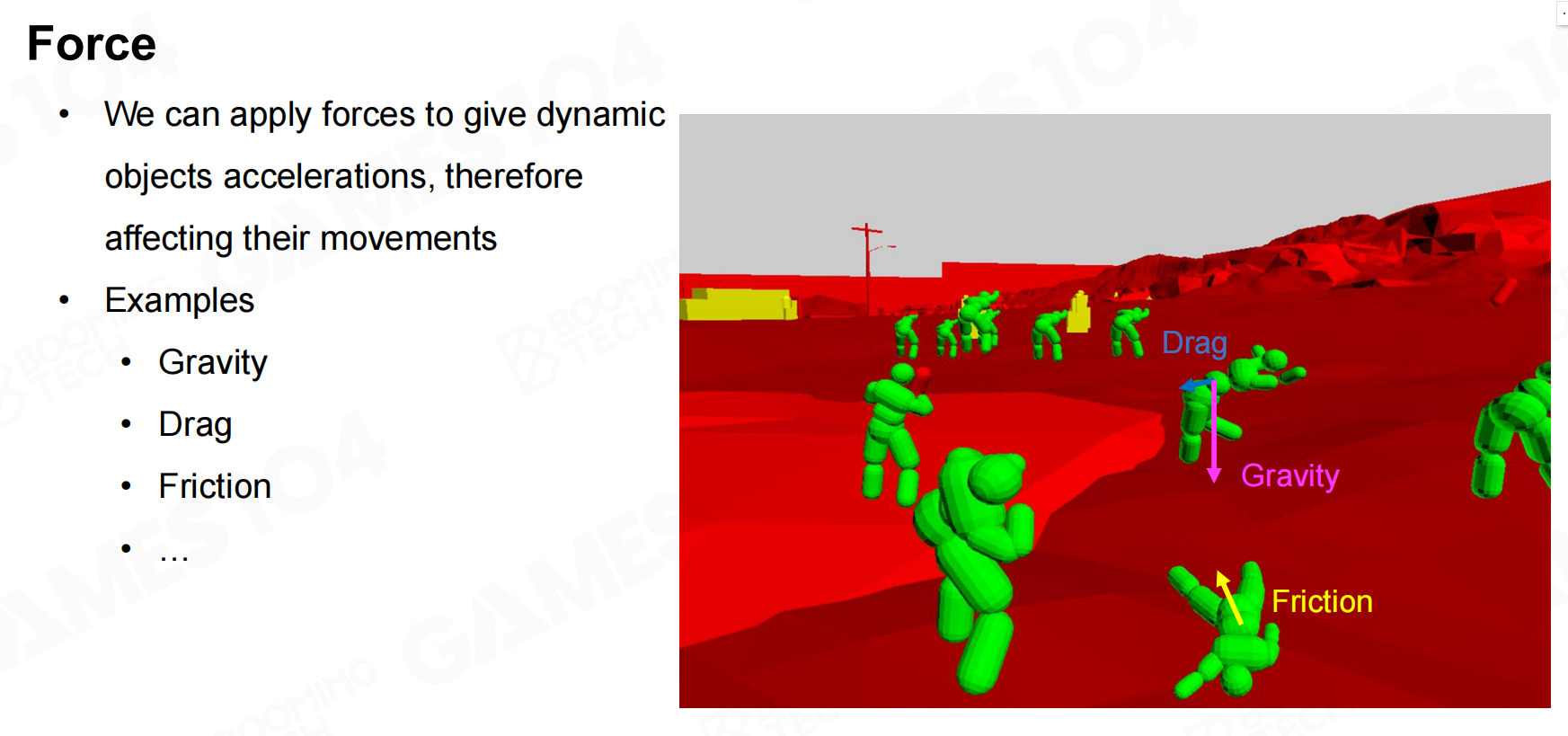
- Impulse 冲量,比如说爆炸导致的冲击力等(虽然其实冲量就是力x时间(恒力条件下))

运动
牛顿第一定律:
在没有外力作用下,物体保持匀速直线运动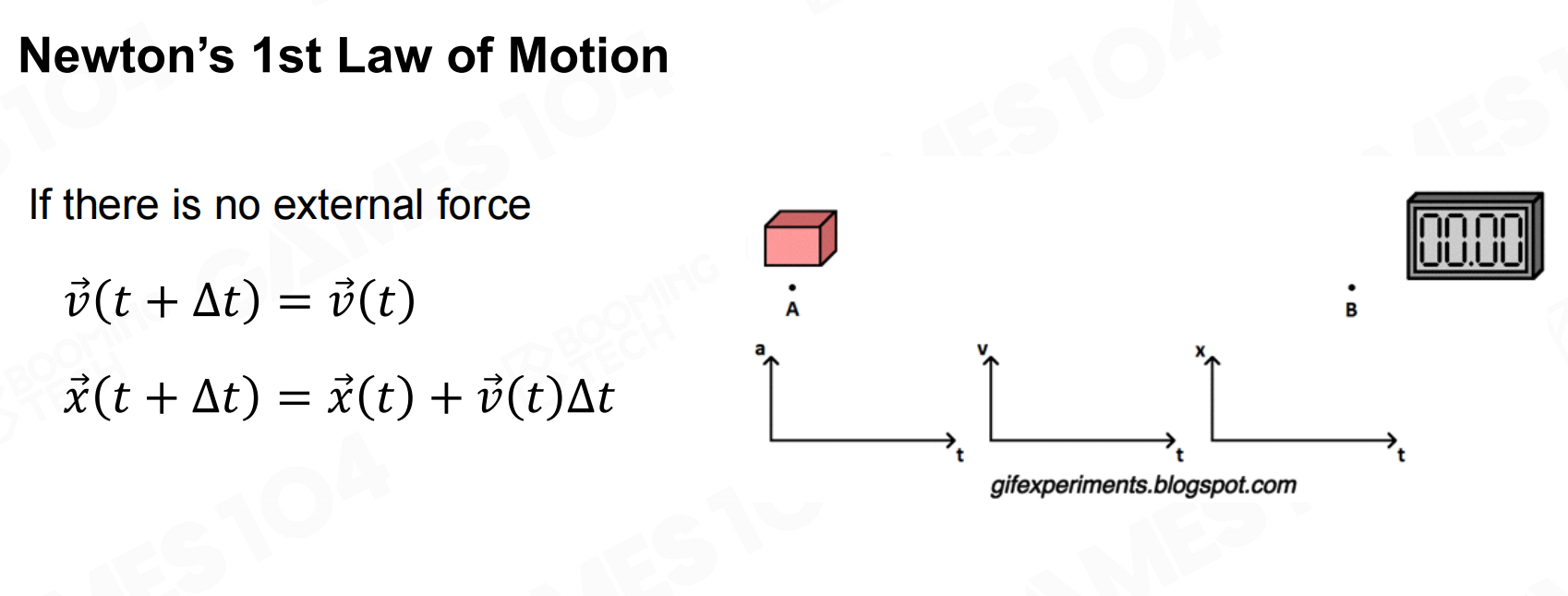
牛顿第二定律:
在有外力作用下,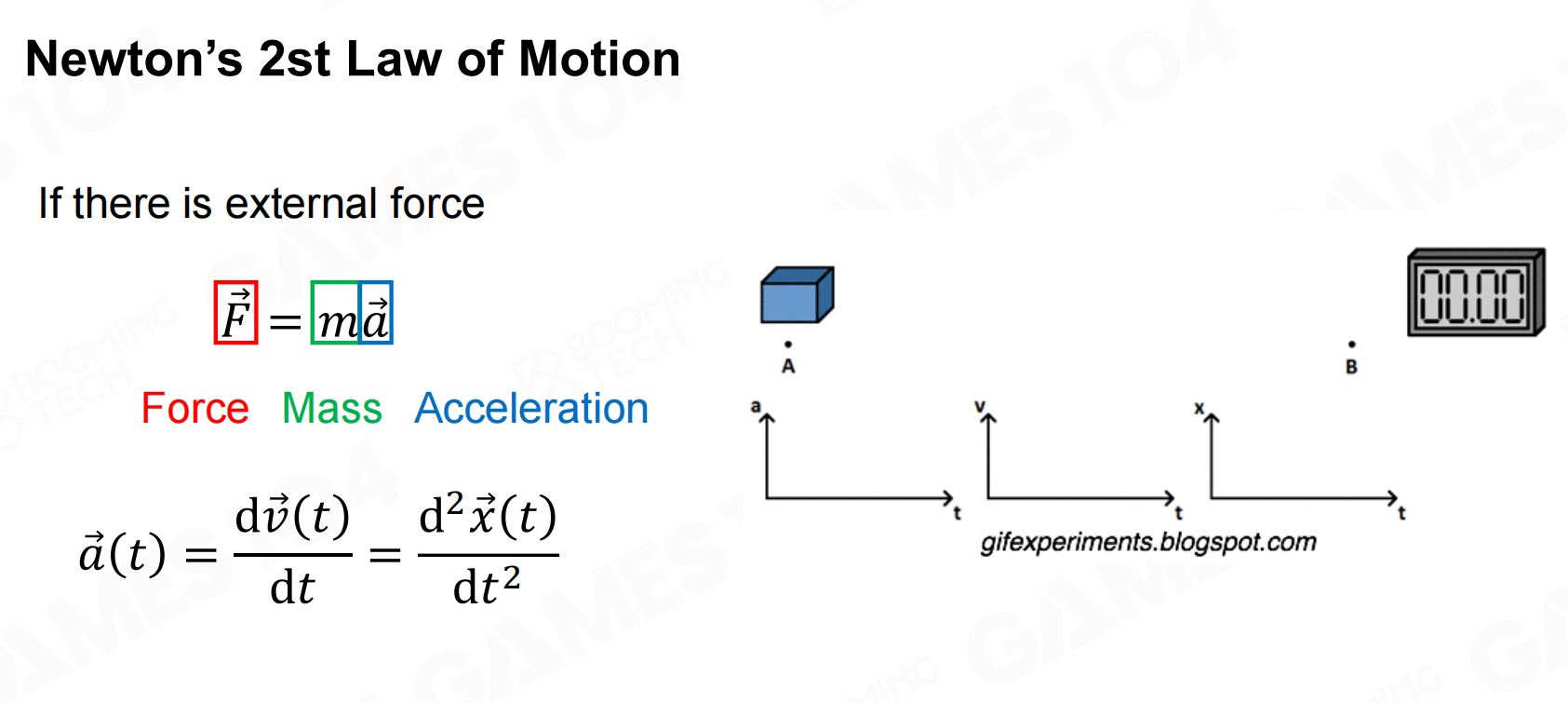
在物理引擎中一般无法使用解析的方式来计算物体的运动,因此我们需要一些数值计算方法来进行求解。
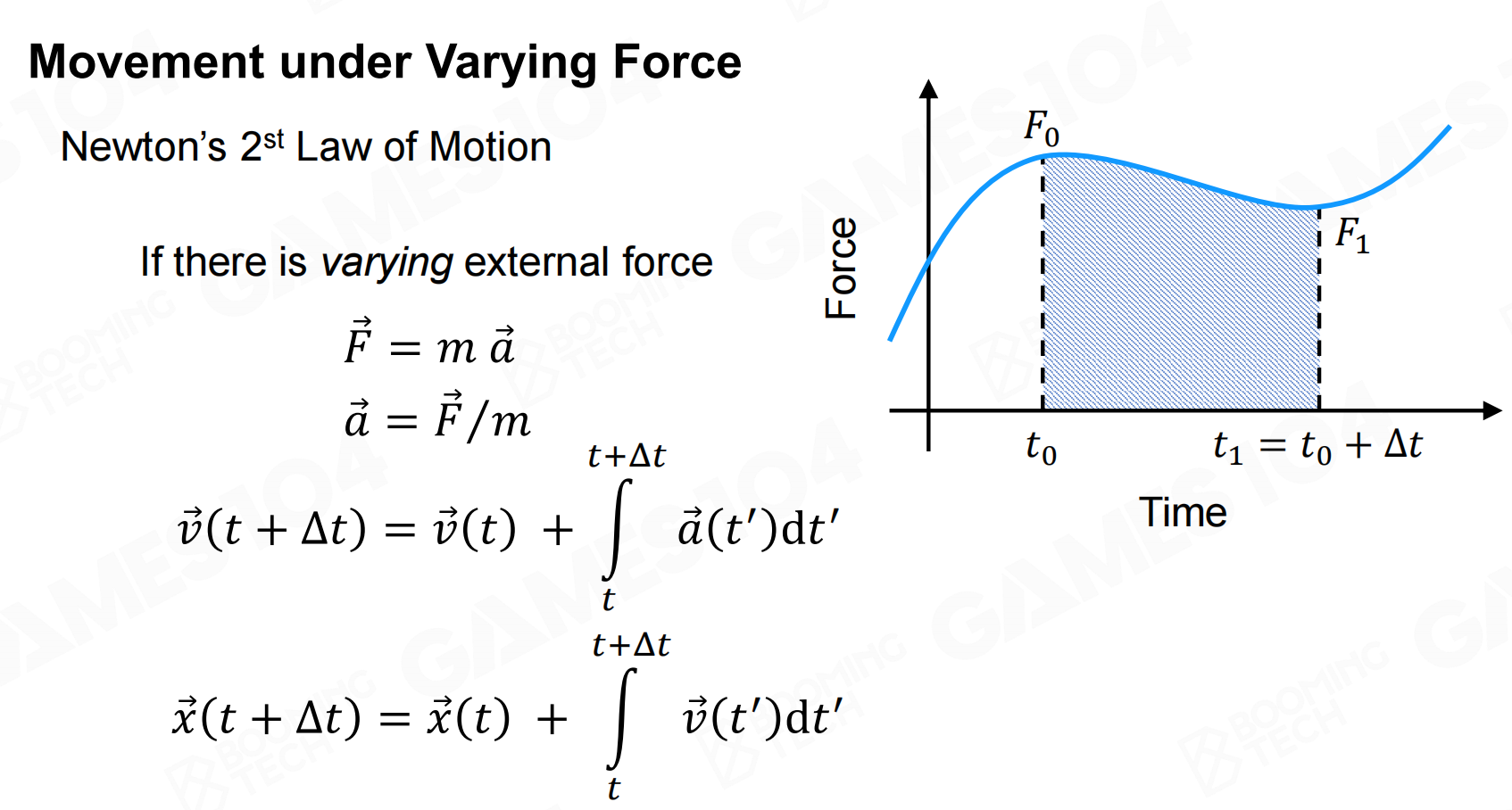
其中上图中
具体以圆周运动为例,如果简单去模拟物体随时间变化,并不是很困难。
但实际游戏中时间不是连续的,而是由一帧帧实现的,所以通常需要解决的问题是在已知当前物体位置和速度的前提下获取之后某时刻的物体位置和速度信息。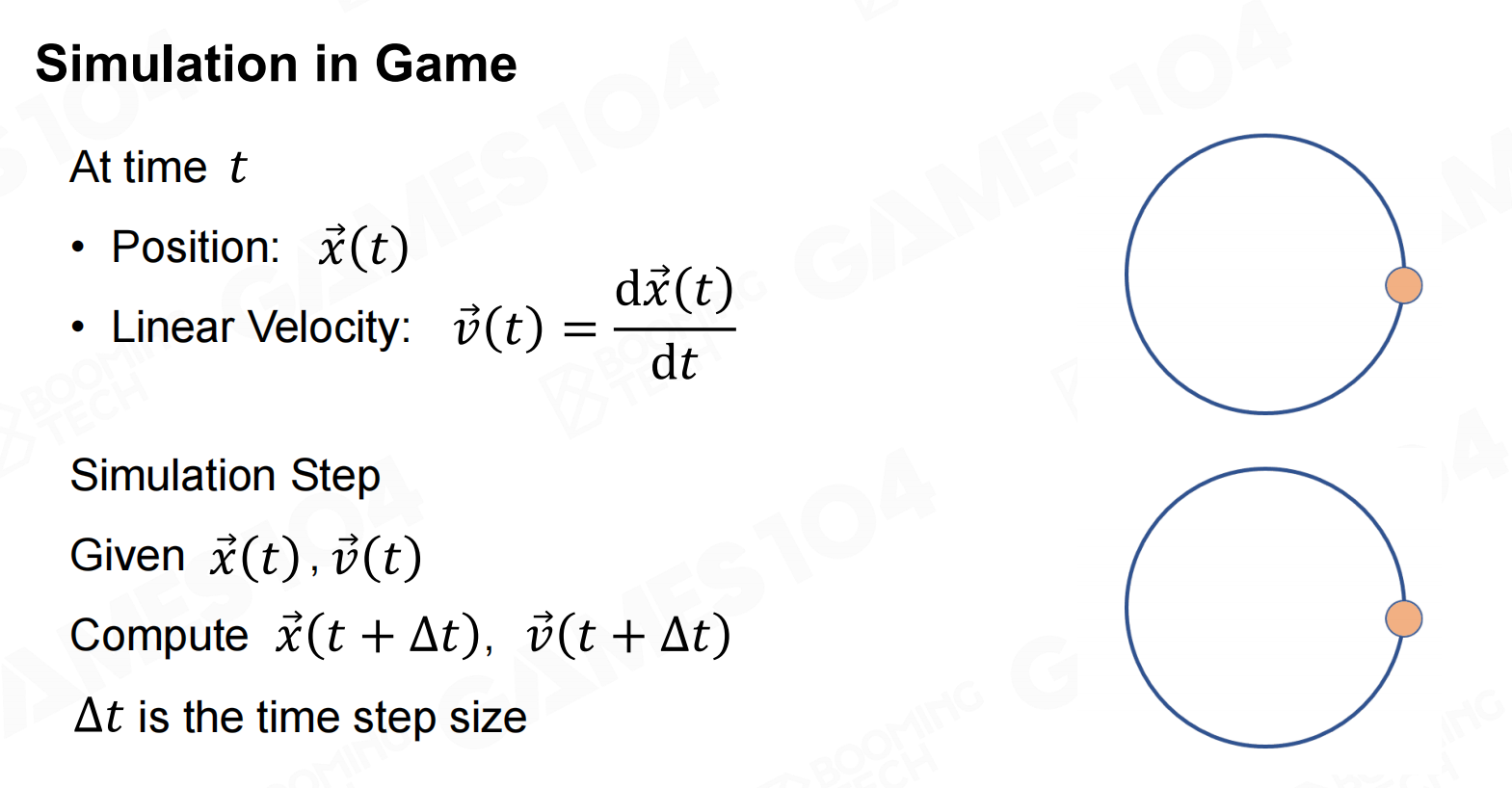
显示欧拉法 Explicit (Forward) Euler’s Method
在进行数值积分时,我们可以把时间间隔设置成一个比较小的值然后对被积函数进行累加来近似实际的积分。
具体来说,在计算物体的运动轨迹时我们首先计算物体在当前位置上受到的力并且积分得到加速度,然后再利用加速度来更新速度以及物体的位置。
这种计算物体运动轨迹的方法称为Euler方法(Euler’s method),也称为显式积分(explicit integration)。
Euler方法实现起来非常简单,但需要注意的是它的本质是使用物体的当前状态来估计下一时刻的运动状态,此时系统的能量是不守恒的。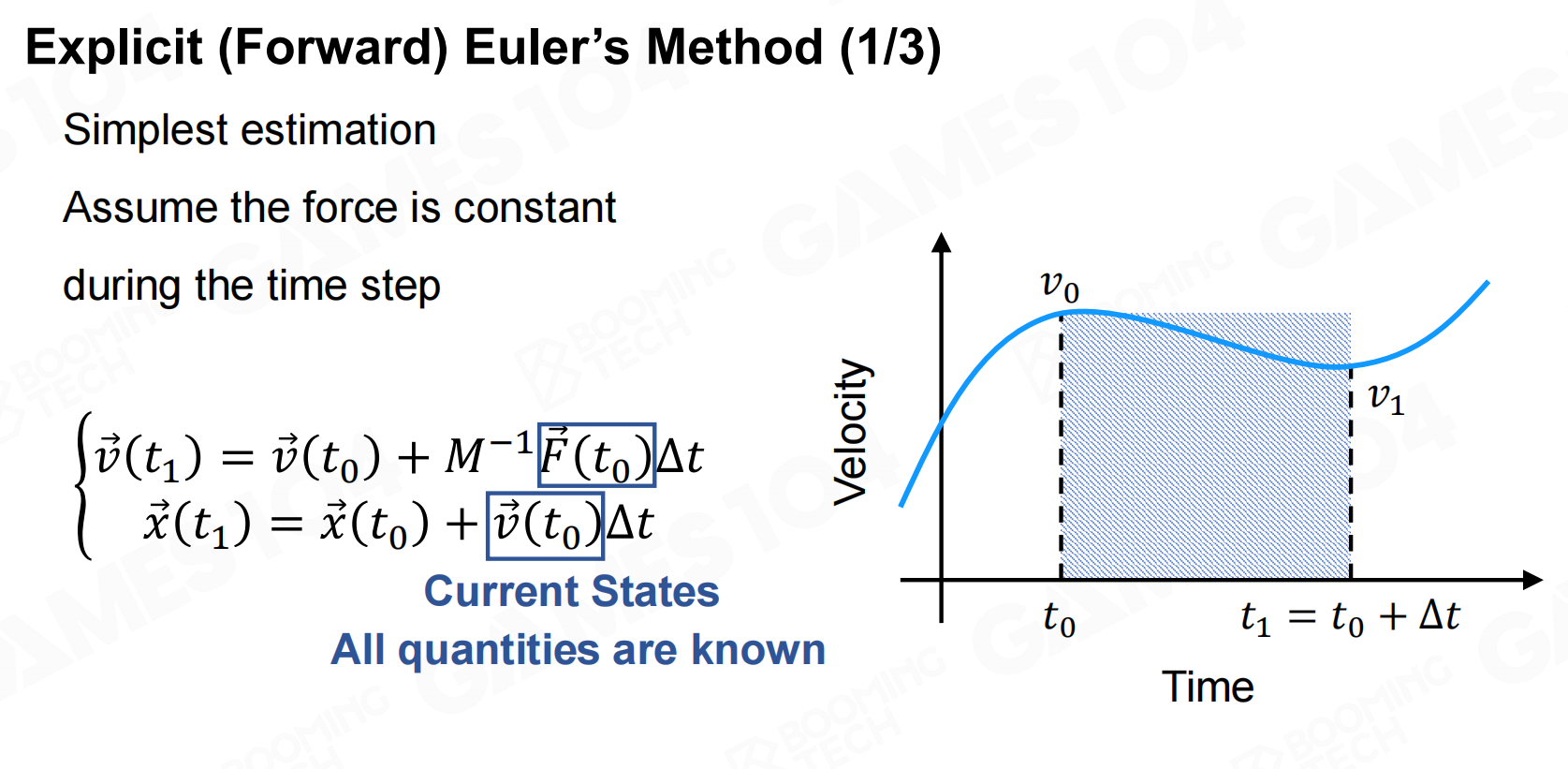
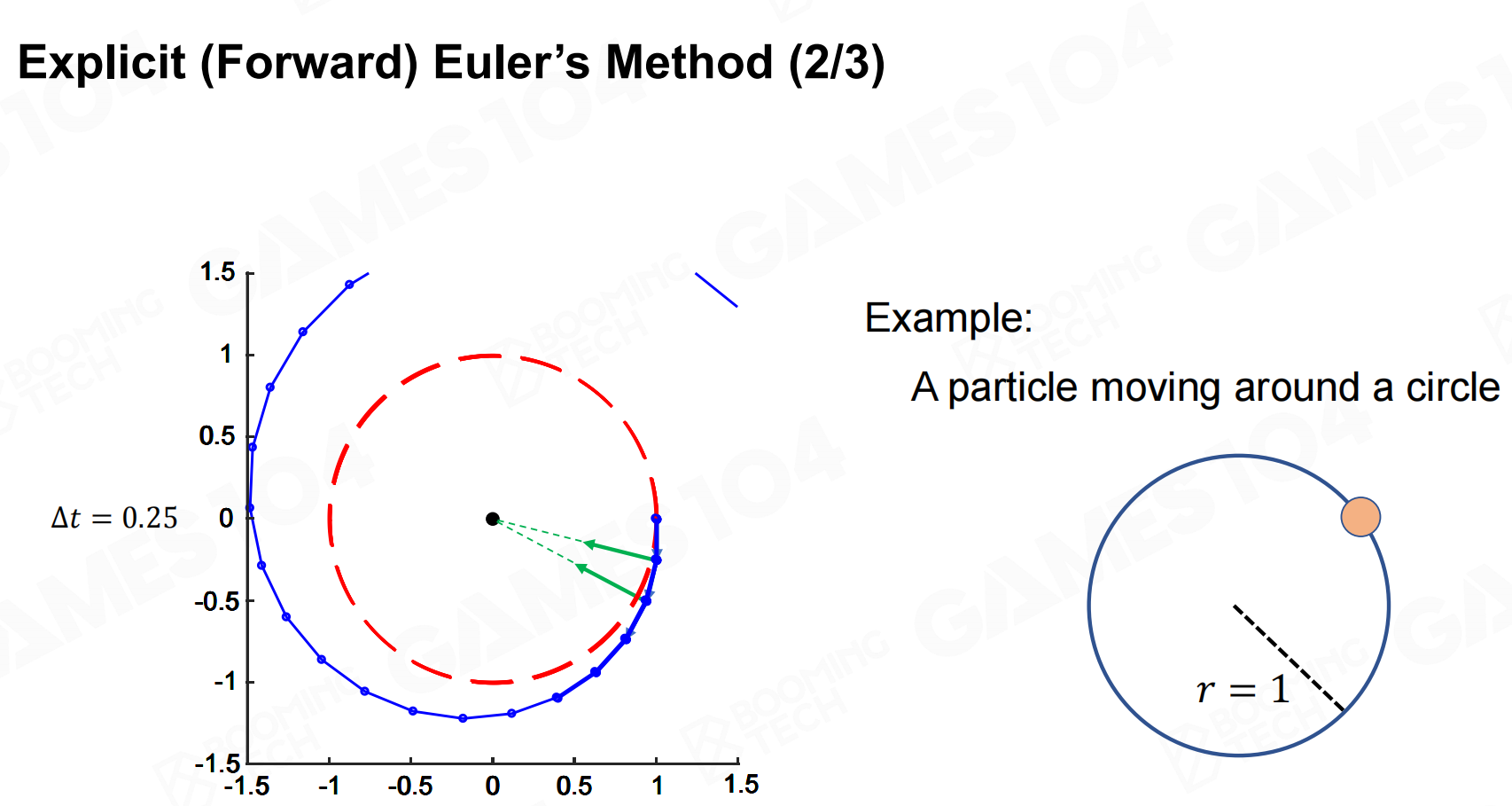
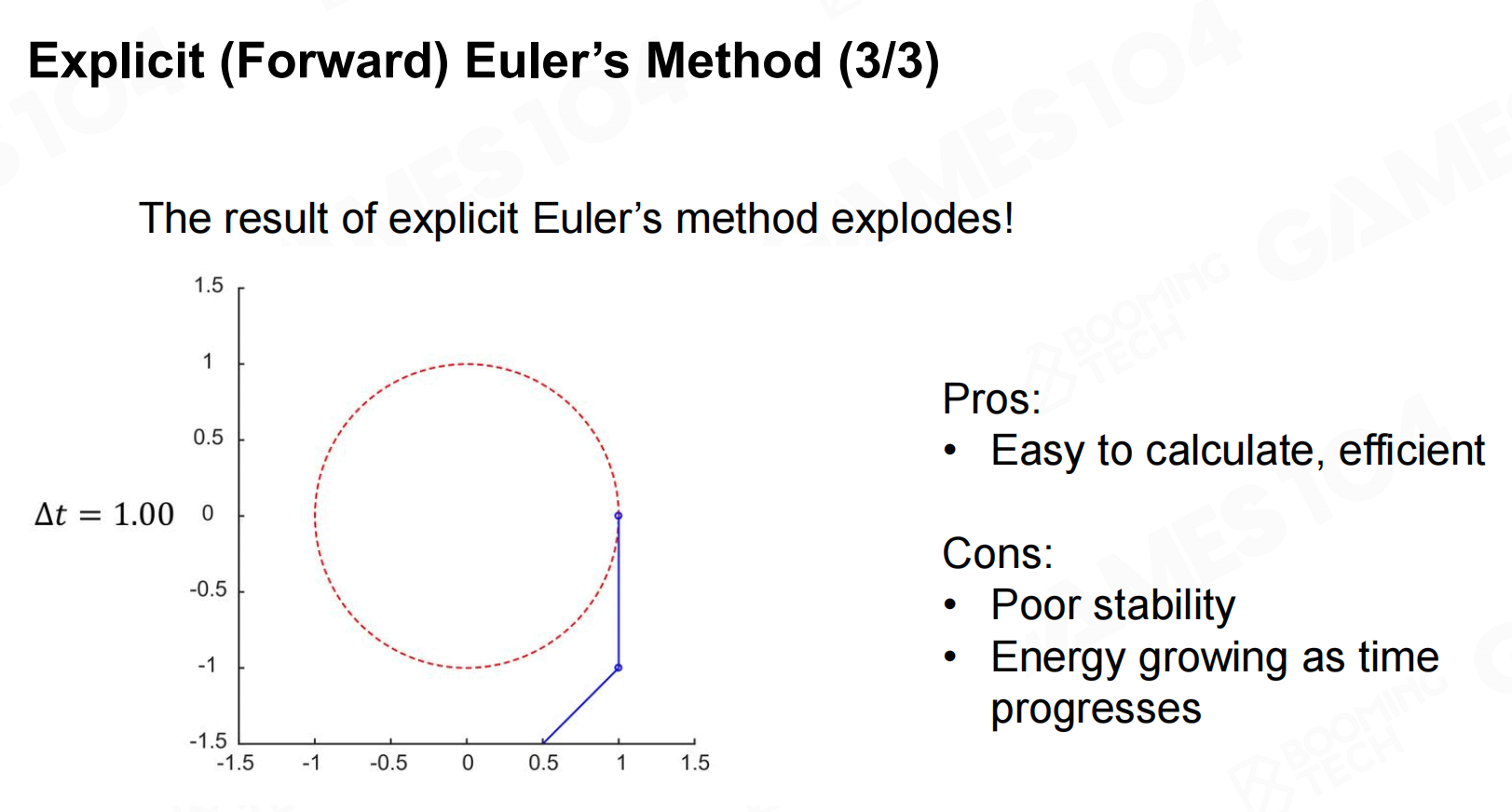
这种方法下,由于实际游戏中的时间片
隐式欧拉法 Implicit (Backward) Euler’s Method
为了提高数值积分的稳定性,人们还开发出了隐式积分(implicit integration)的技术。
隐式积分的实现也很简单,只需要在求解加速度和速度时使用下一时刻而不是当前时刻的值即可, 同时可以证明此时系统的能量会不断衰减。
当然这又引入了另一个问题,即如何计算系统在下一时刻的物理量, 这在很多情况下是比较困难的。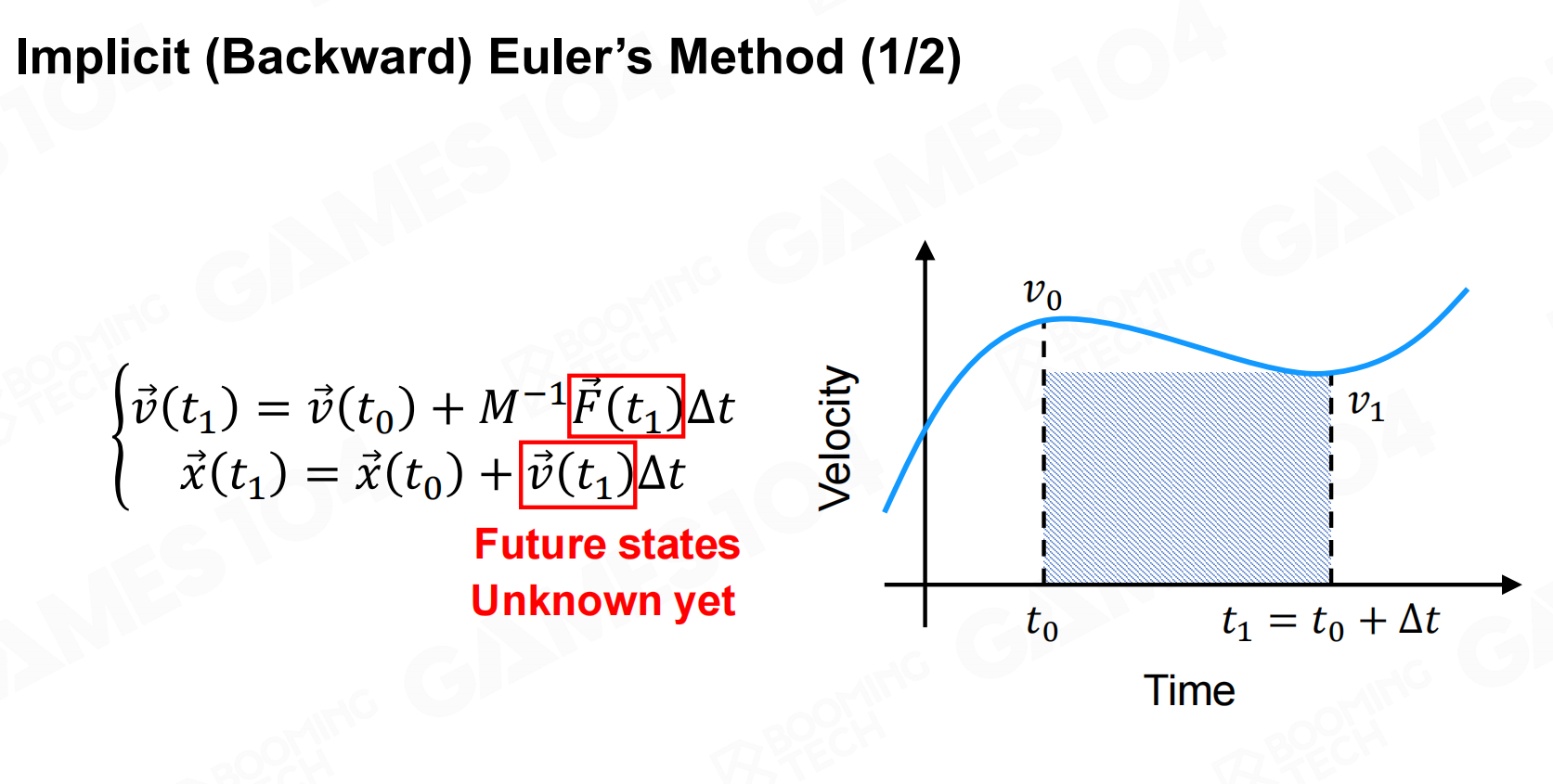
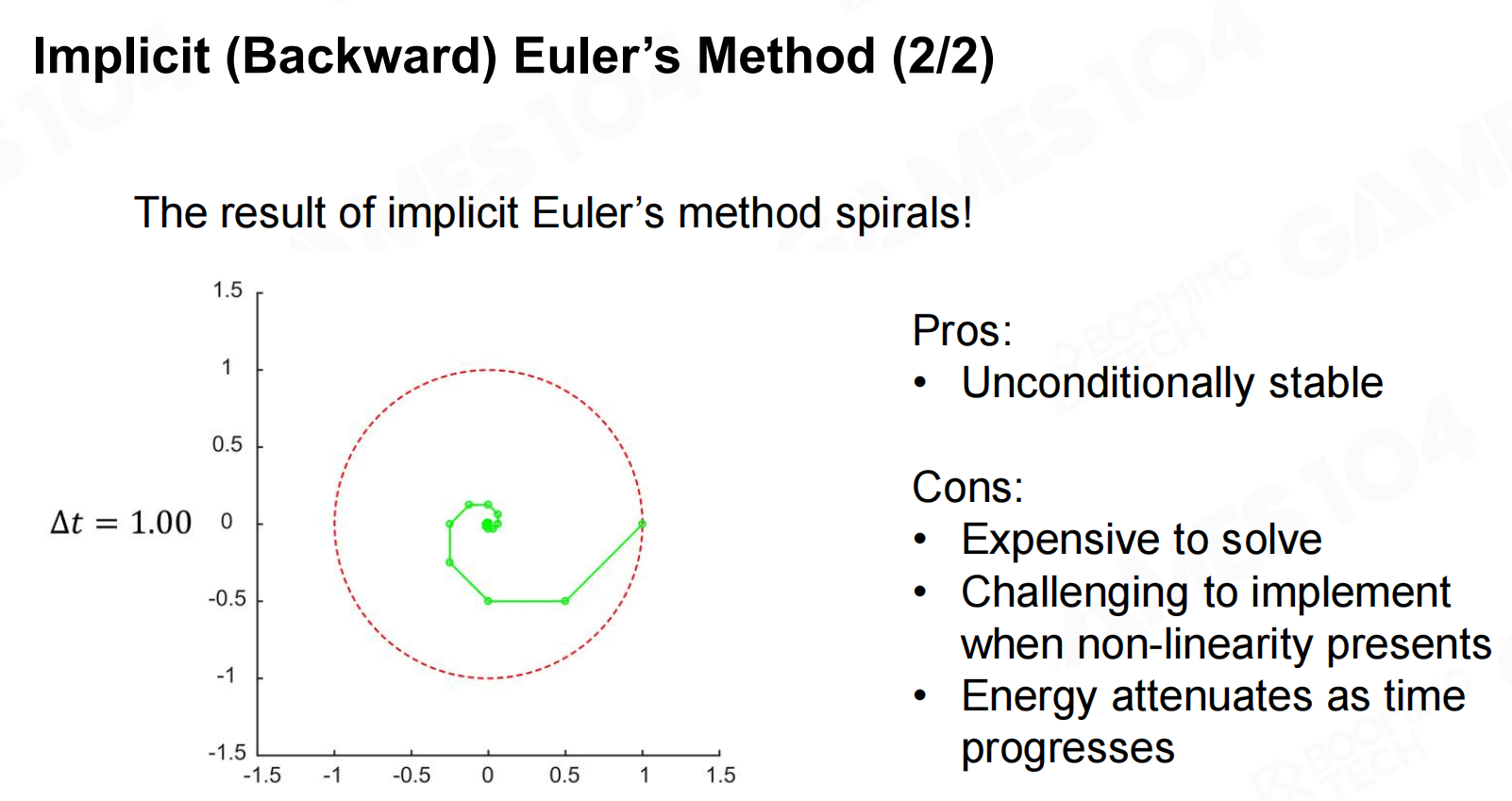
其中未来的值是假设能够通过解析解强行算出来的。 和显示方法类似,该方法的问题是能量会衰减,
但由于这个衰减相对较慢,所以用户可能会认为是摩擦力、空气阻力等其他力的影响导致,
从而使得这个衰减在游戏实际中相对不明显。 从另一个角度来说,我们在游戏引擎中设计中认为衰减肯定是好过增多的,
前者顶多最后停下来,但后者会不可控会爆炸。 通过一系列复杂计算可以证明这种隐式方法是无条件稳定的。 但其缺点是:
- 计算成本高(计算未来值)
- 运动非线性时难以计算
- 能量衰减。
半隐式欧拉法 Semi-implicit Euler’s Method
在游戏引擎中更常用的积分方法是半隐式Euler方法(semi-implicit Euler’s method),
即在计算加速度时使用当前时刻的力推导下一时刻的速度,而在计算位置时使用刚才计算出的速度再更新位置。
半隐式方法有非常高的数值稳定性,广泛应用于各种类型的物理仿真中。
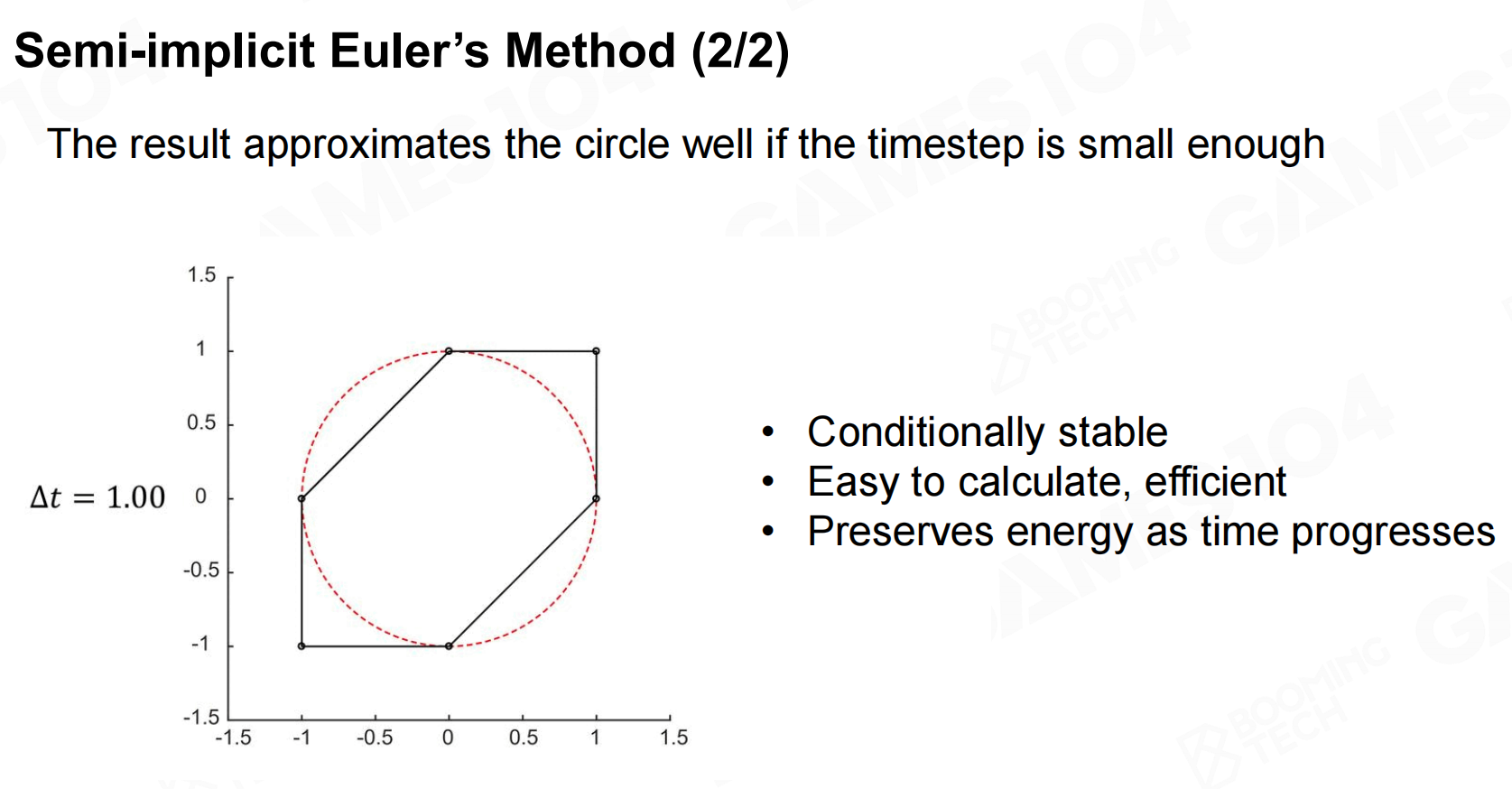
计算未来速度时用当前的力,计算未来位移时用未来的速度。 前提假设:力是不变的(很危险的假设,因为实际上力跟物体位置是相关的)。
优点是:
- 条件性稳定
- 计算简单有效
- 随着时间的推移能够保存能量
缺点是做一些sin cos等运动时,积分出来的周期会比正确值长一点点,所以在相位上会有偏移差。
刚体动力学
有了牛顿定律和数值积分算法就可以开始进行物理仿真了,其中最简单的情况是质点动力学(particle dynamics)。
在质点动力学中所有的物体都被抽象为没有具体形状的质点,此时我们只需要按照牛顿定律更新质点的运动状态即可。
在游戏引擎中更为常见的仿真场景是刚体动力学(rigid body dynamics)。 和质点动力学不同,
刚体动力学仿真需要考虑物体自身的形状,也因此需要在质点运动的基础上引入刚体旋转的相关概念。
取向
刚体的朝向(orientation)可以使用一个旋转矩阵或者四元数来表示,它表示刚体当前姿态相对于初始姿态的旋转。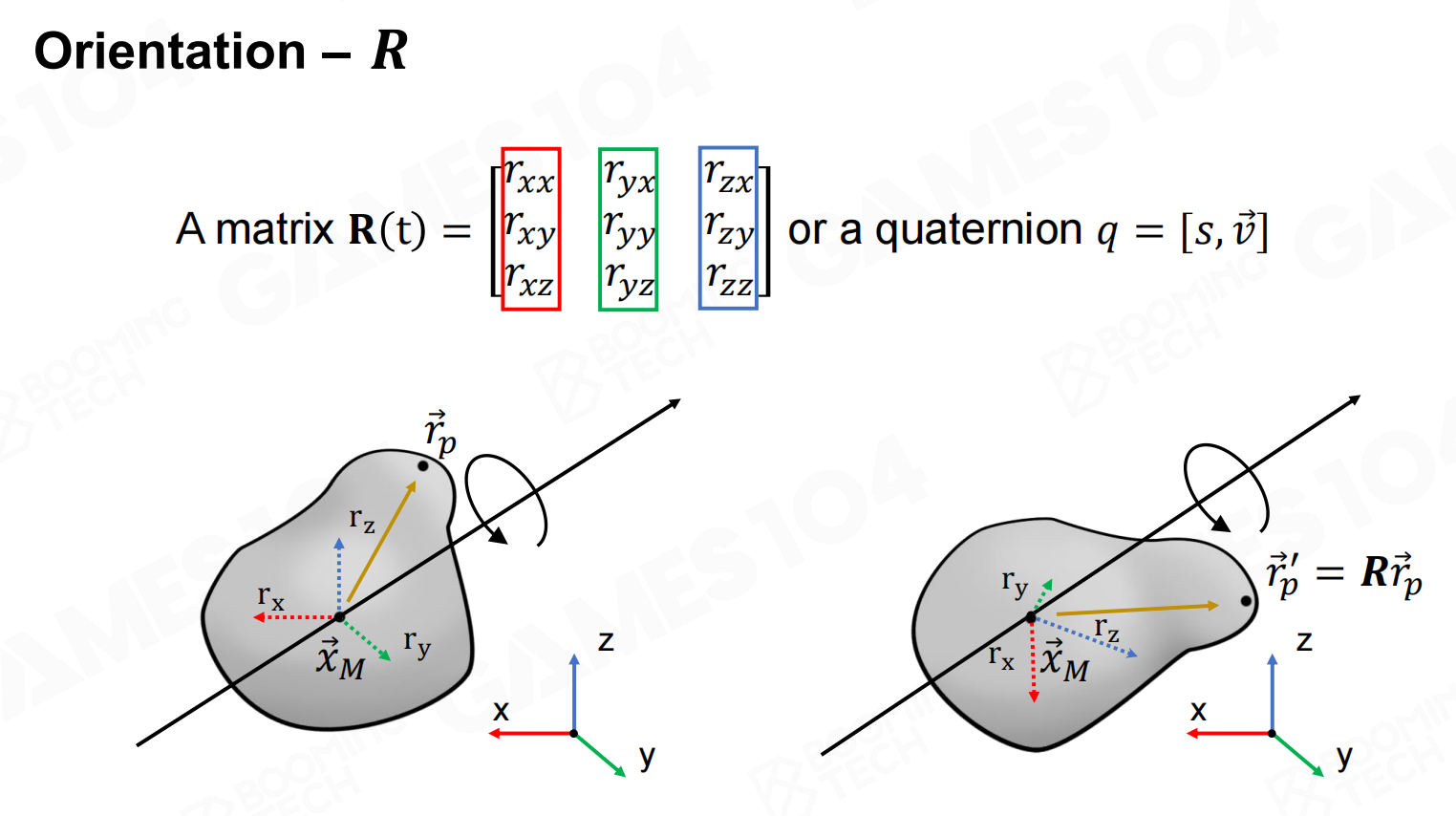
角速度
角速度(angular velocity)表示刚体绕某个旋转轴旋转的速度,需要注意的是在描述角速度时必须要指明旋转轴。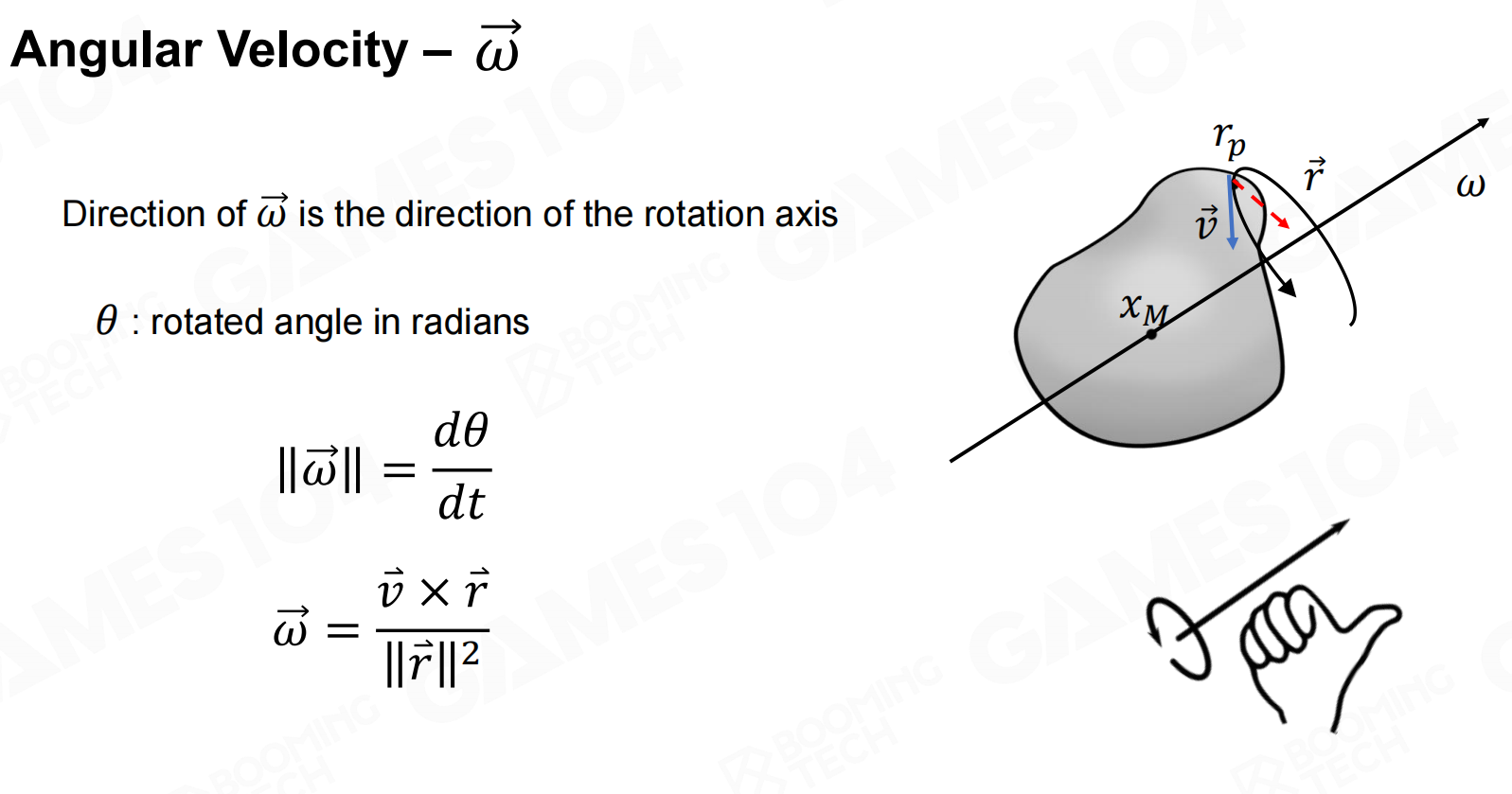
角加速度
角加速度(angular acceleration)类似于加速度,不过它描述的是角速度的变化。
这里需要说明的是角速度的变化不仅包括绕当前轴转速的变化,它还包括旋转轴发生变化的情况。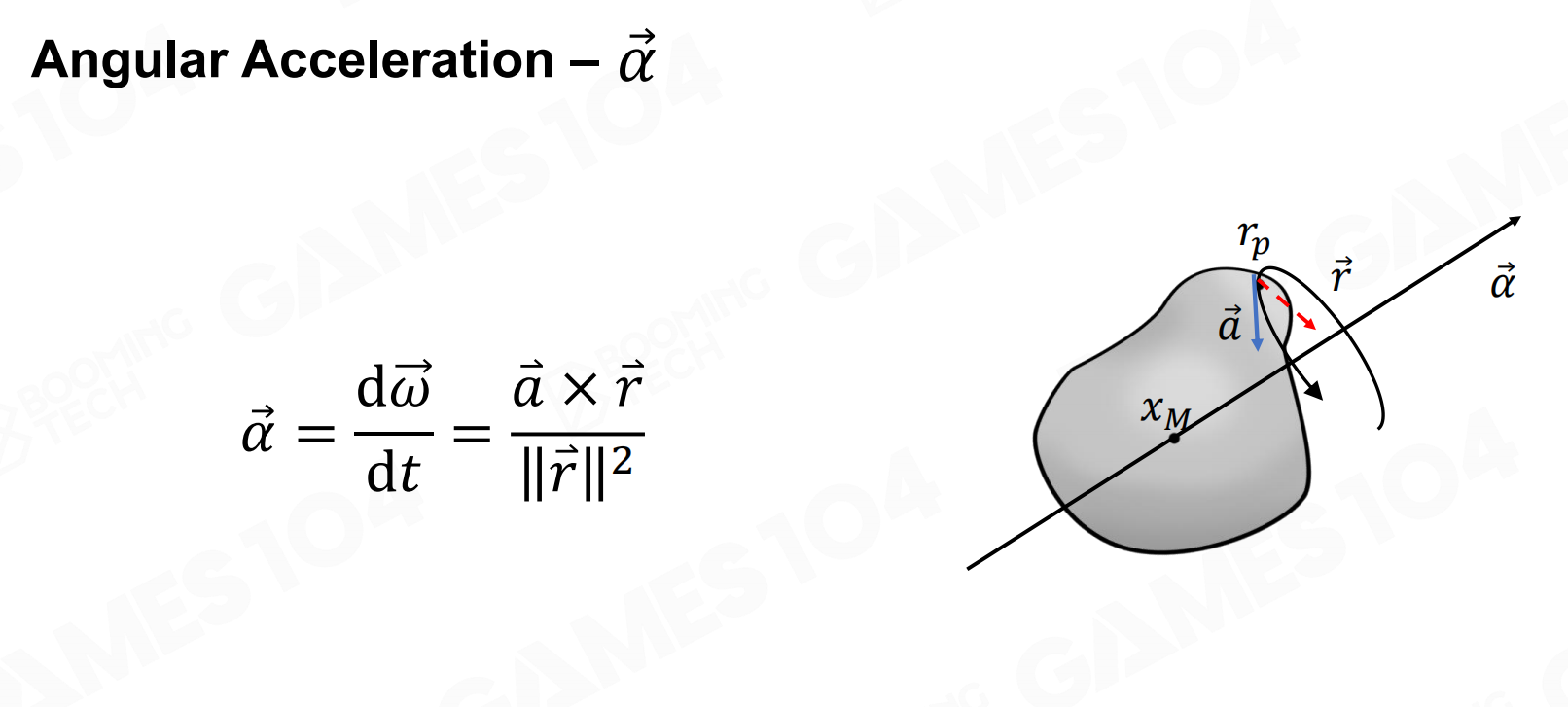
旋转惯量
转动惯量(rotational inertia)类似于质量,它描述了刚体抵抗旋转的能力。 转动惯量与质量的一大区别在于转动惯量不是一个常数而是一个张量(矩阵),
当刚体的朝向发生改变时需要利用旋转矩阵来计算当前姿态下的转动惯量; 同时转动惯量也与刚体上的质量分布密切相关。

角动量
角动量(angular momentum)则描述了刚体旋转的状态,它是转动惯量与角速度的乘积。
力矩
当外力不通过刚体的质心时会产生力矩(torque),从而导致刚体发生旋转。
在质点动力学的基础上把旋转部分也考虑进来对物体的运动状态进行更新就得到了刚体动力学的仿真方法。
应用:台球动力学
以台球游戏模拟为例,我们假设台球自身与桌面没有摩擦,这样台球的运动可以简化为二维平面运动。
在进行仿真时需要把球杆给予台球的力(冲量)移动到球心来计算台球沿球杆方向的速度;
同时这种移动还会对台球施加一个力矩使台球产生旋转,因此也需要更新台球的角速度。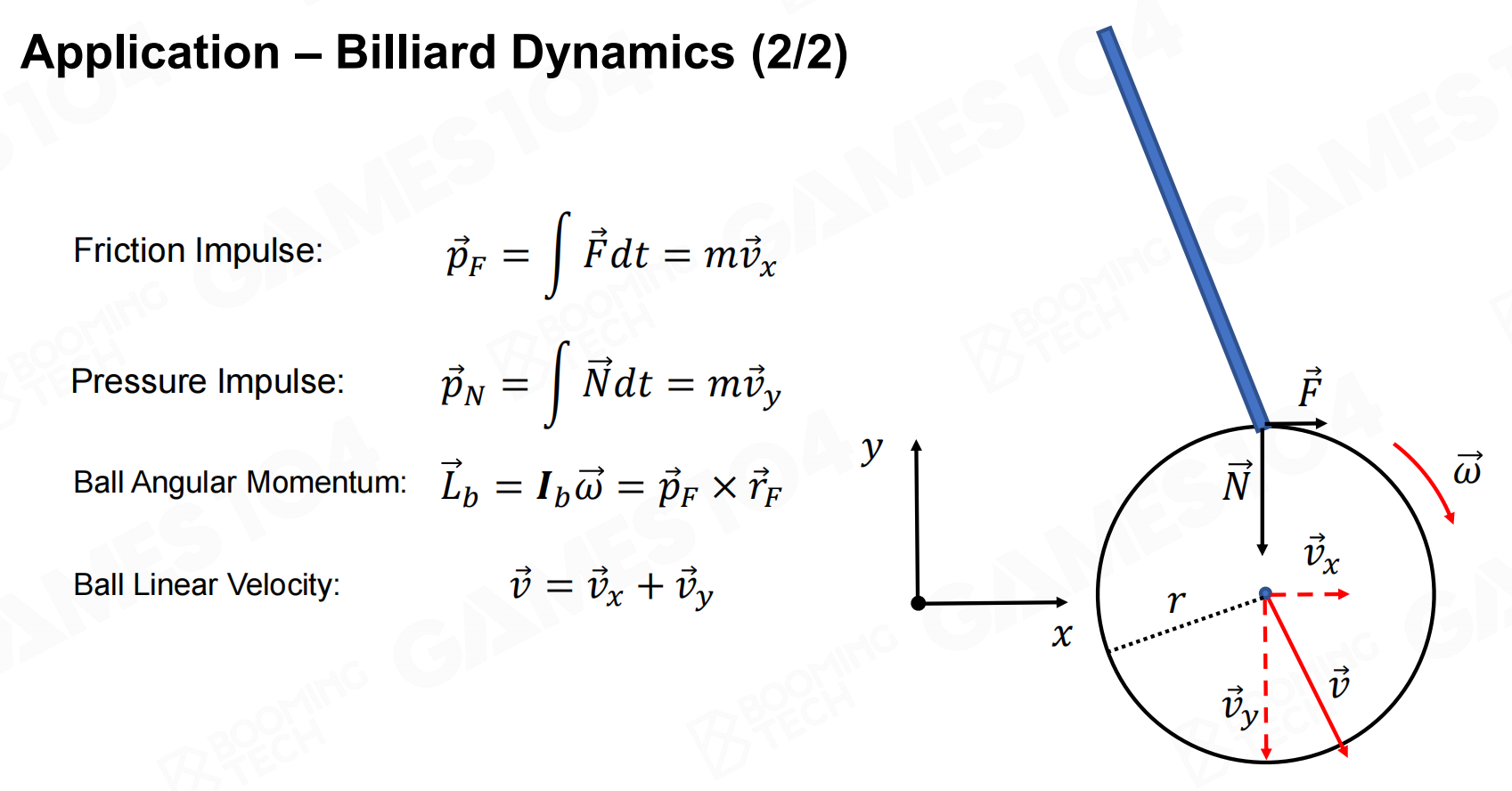
碰撞检测
在进行刚体仿真时我们需要考虑不同刚体之间的相互作用,也即所谓的碰撞问题。
要求解碰撞问题的第一步是对刚体碰撞进行检测,目前在物理引擎中注意是使用两阶段的检测方法。
碰撞检测一般分为两个阶段
- Broad phase 初筛 – 利用AABB等找到刚体有没有相交
- Narrow phase – 获取进一步信息(碰撞点、方向、深度等)
Broad Phase一般常见的有两种方法:
- BVH Tree – 更新成本低,适合动态场景。
- Sort and Sweep – 先排序再逐个扫描,效率高,更符合大部分为静态物体小部分为动态物体的现实。更好。

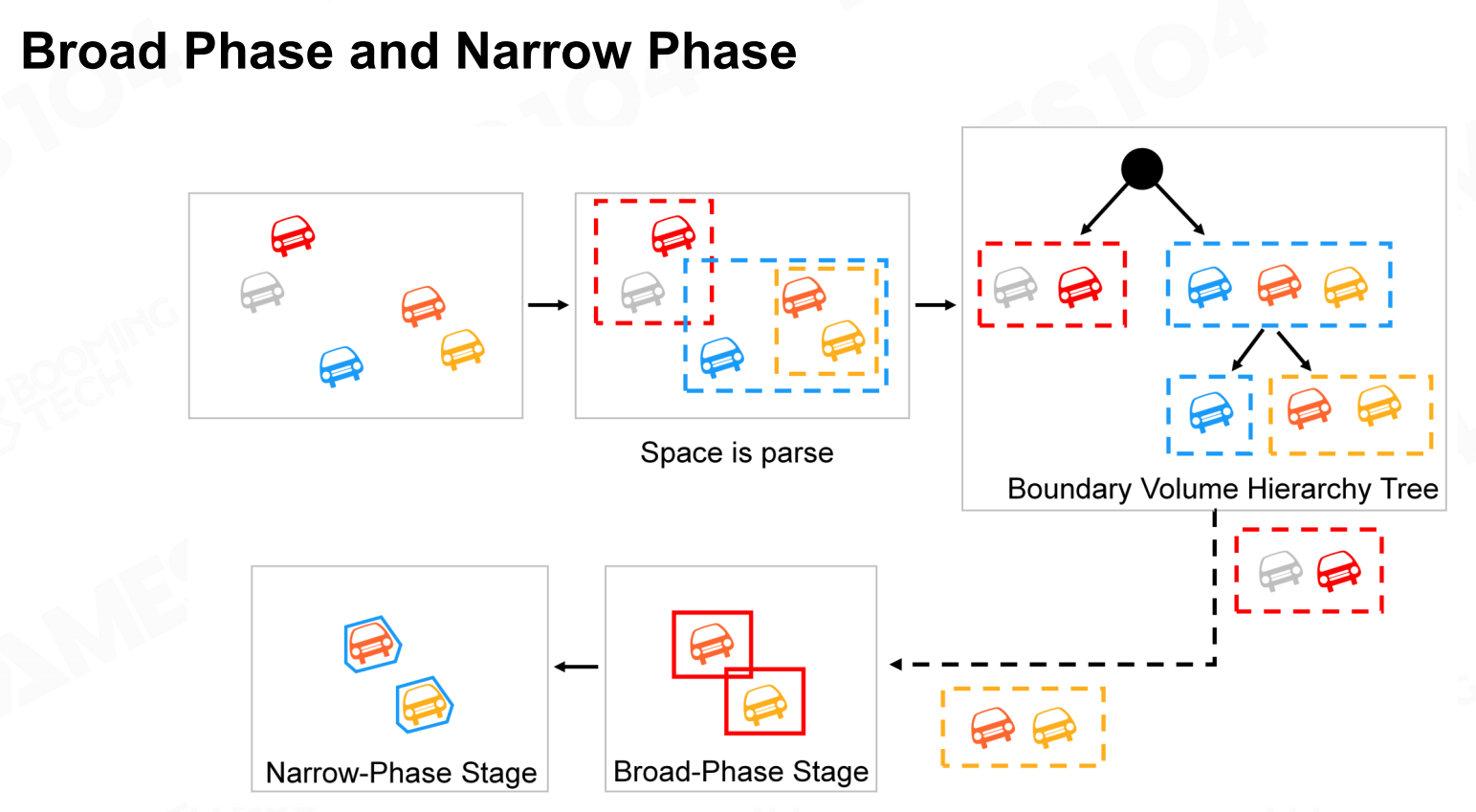
宽相
显然场景中大部分的物体是不会同时发生接触的,因此所谓的broad phase就是只利用物体的bounding box来快速筛选出可能发生碰撞的物体。
目前物理引擎中常用的碰撞检测包括空间划分(space partitioning)以及sort and sweep两类方法。
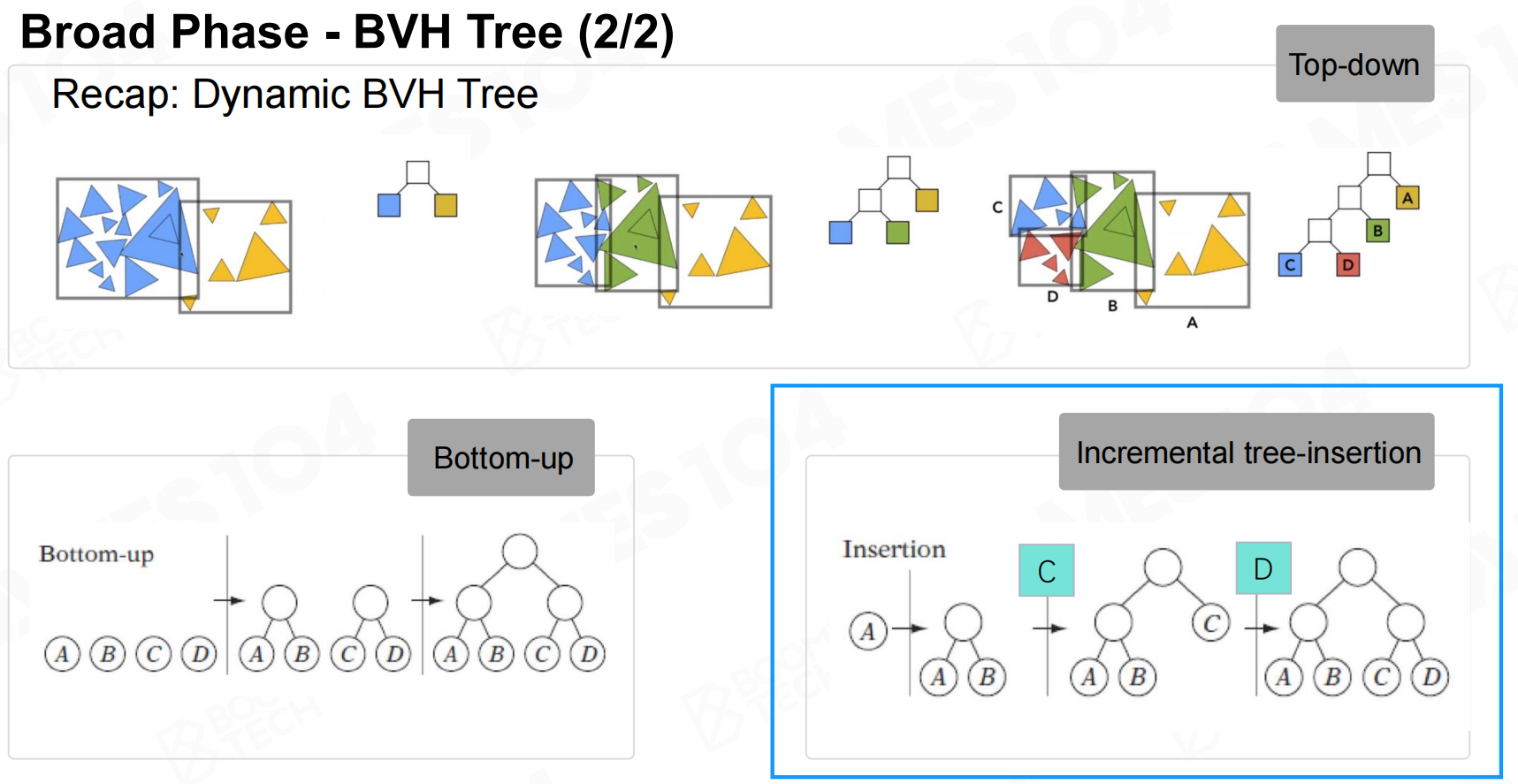
BVH树
我们在介绍渲染技术时就介绍过空间划分的相关概念,它的思想是把场景中的物体使用一个树状的数据结构进行管理从而加速判断物体是否相交的过程。
BVH是空间划分的经典算法,它使用一棵二叉树来管理场景中所有物体的bounding box。 BVH的特点是它可以通过动态更新节点来描述场景中物体的变化,
因此可以快速地检测场景中的bounding box可能存在的碰撞。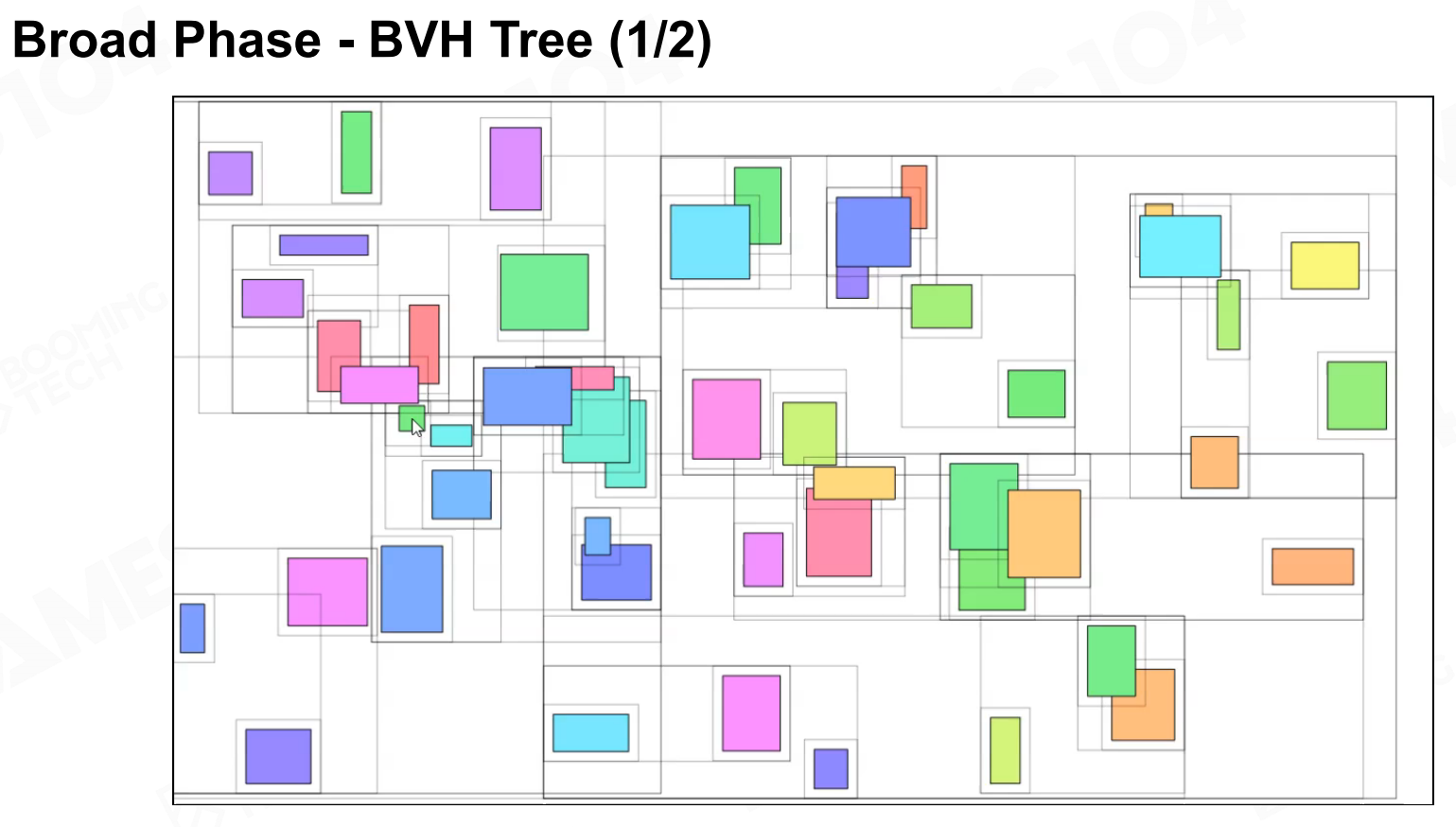
排序和扫描
sort and sweep是使用排序来检测碰撞的算法。 它的思想非常直观:对于使用AABB进行表示的bounding box,
两个bounding box出现碰撞时必然会导致它们的边界产生了重叠,而判断是否出现重叠则可以通过对bounding box的边界进行排序来进行计算。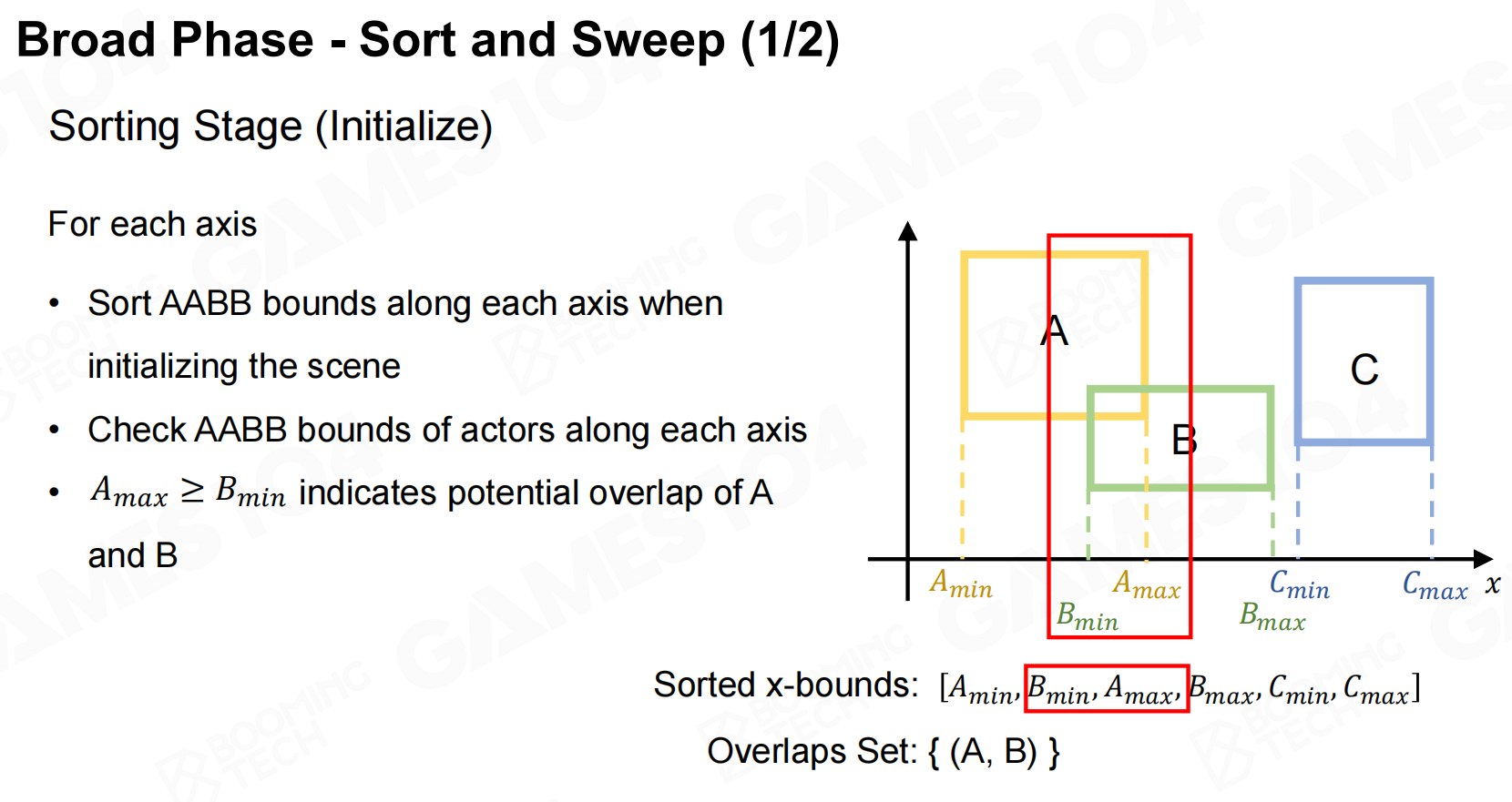
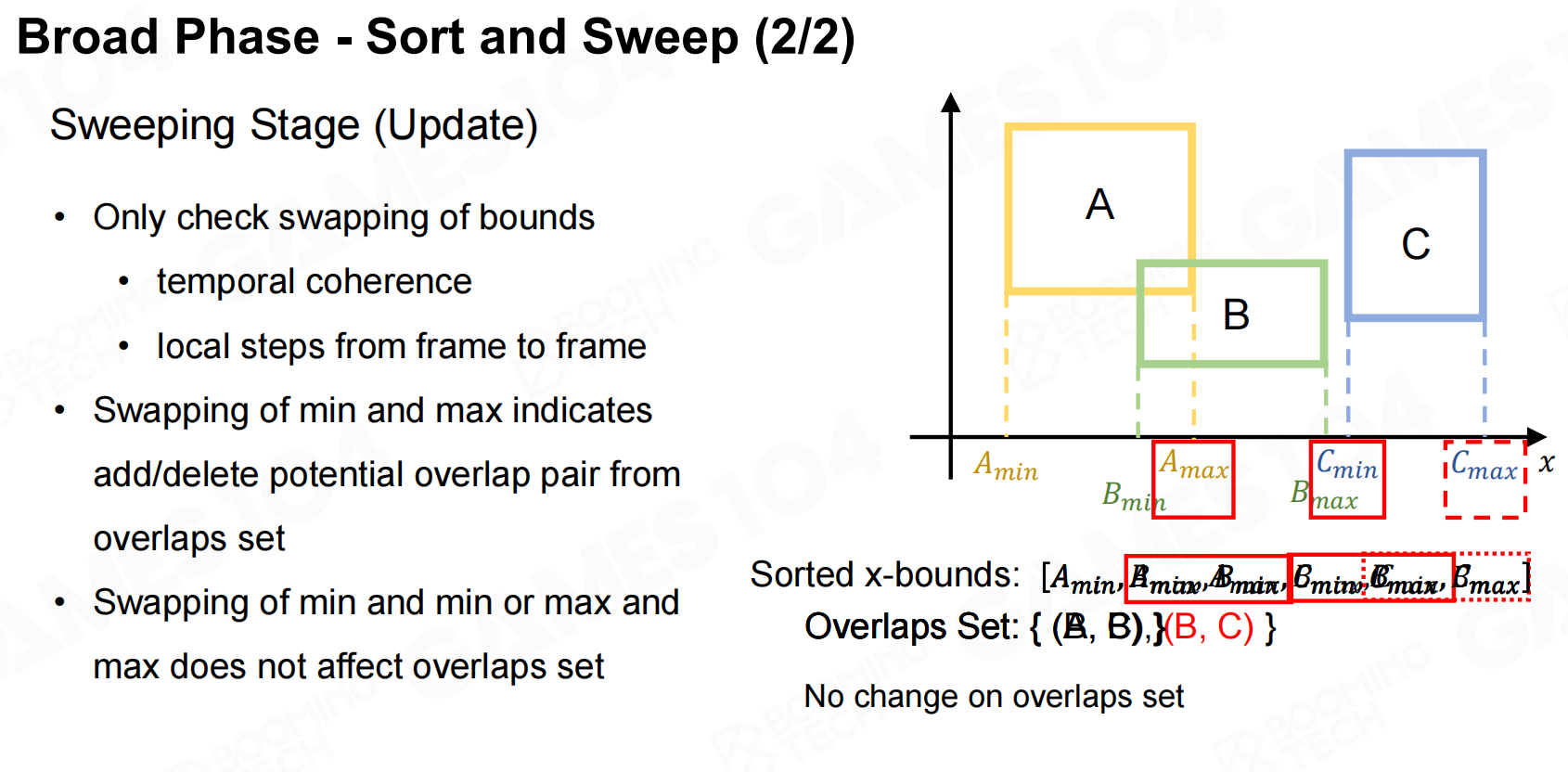
窄相
筛选出可能发生碰撞的物体后就需要对它们进行实际的碰撞检测,这个阶段称为narrow phase。 除了进一步判断刚体是否相交外,
在narrow phase中一般还需要去计算交点、相交深度以及方向等信息。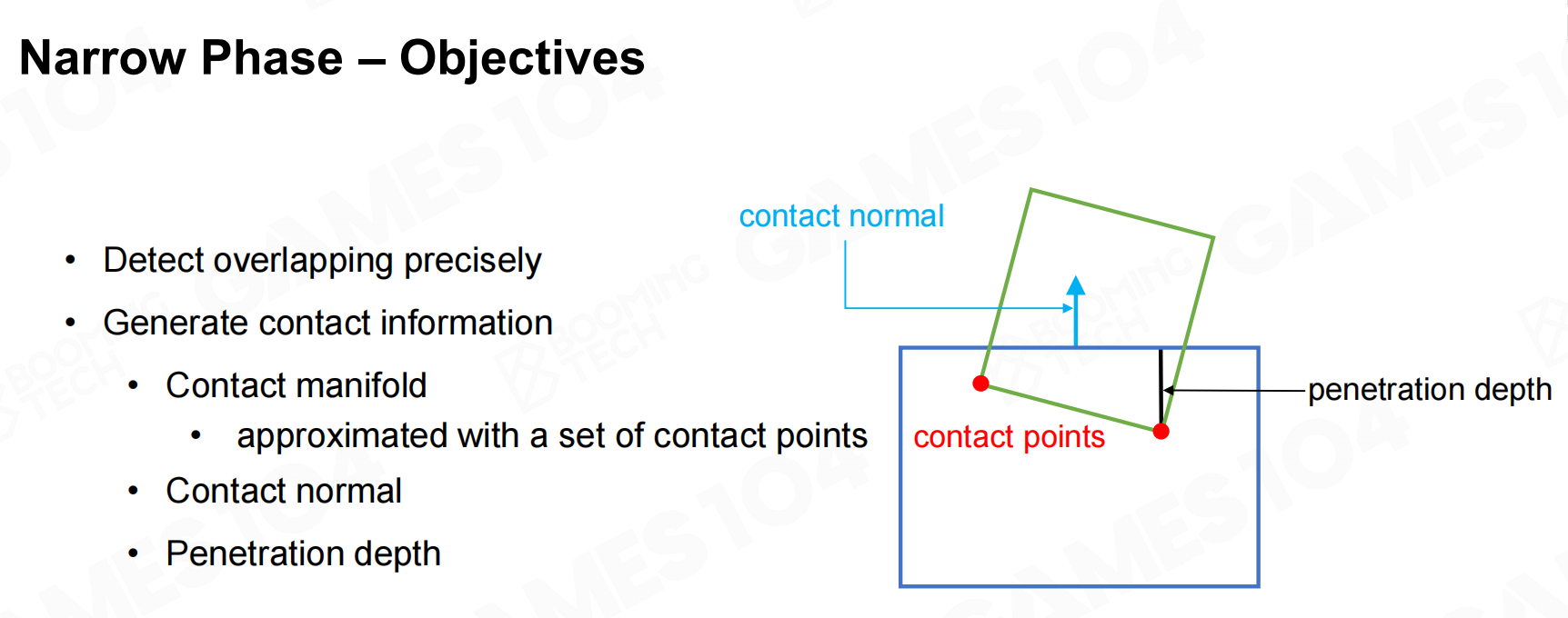
目前在narrow phase中一般会使用相交测试、Minkowski距离以及分离轴等方法。
基本形状相交测试
对于一些简单的几何形状可以使用解析的方法来判断它们是否相交并且计算交点的信息。


闵可夫斯基基于差分的方法
对于凸多边形的情况则可以使用Minkowski差异(Minkowski distance)来判断它们是否相交。
在介绍Minkowski距离之前首先要引入Minkowski和(Minkowski sum)的概念:
对于两个点集
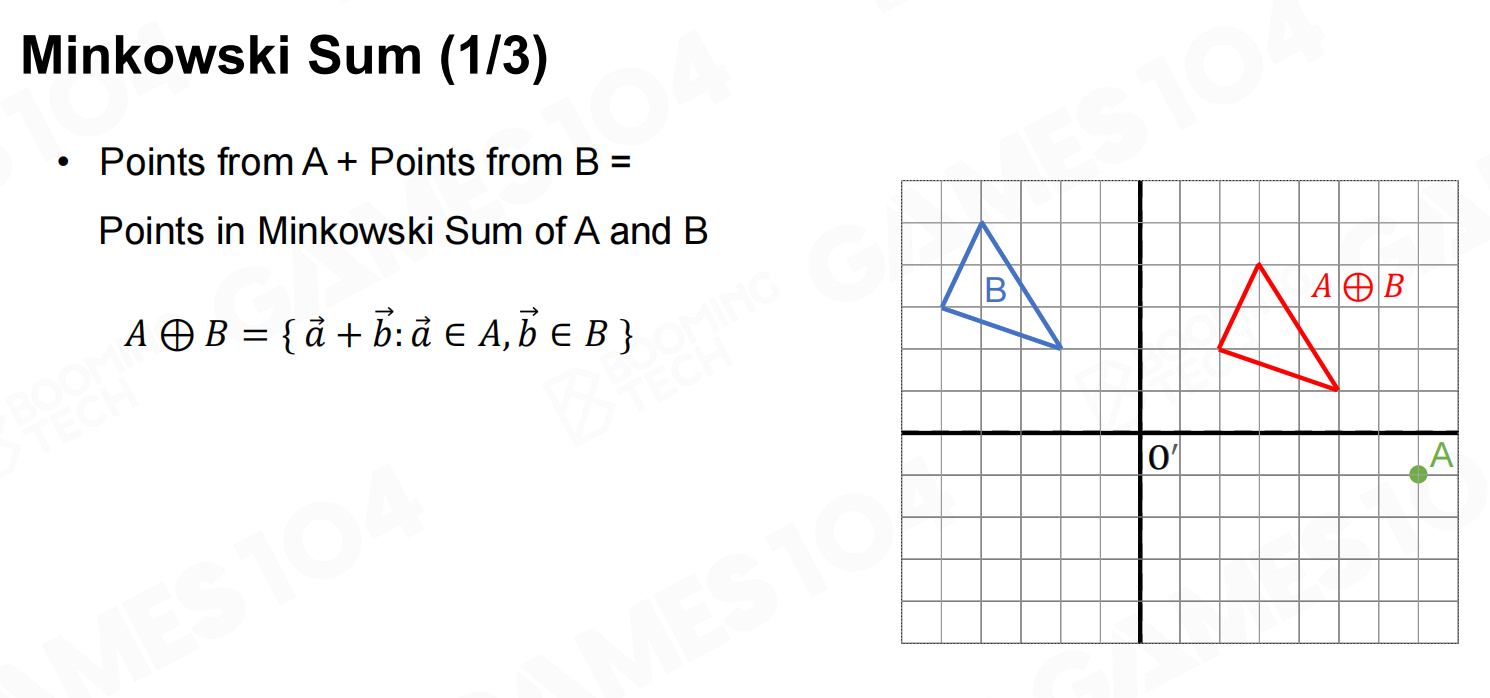
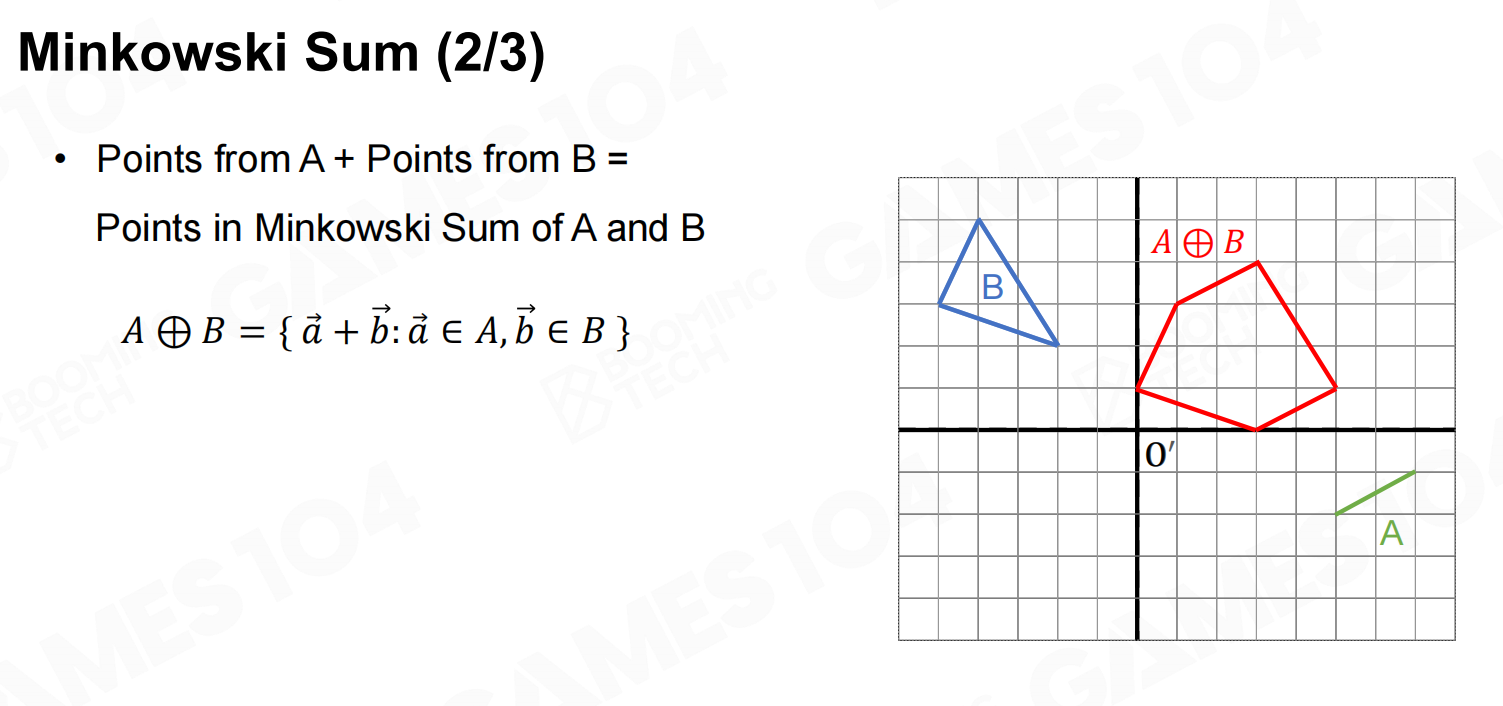
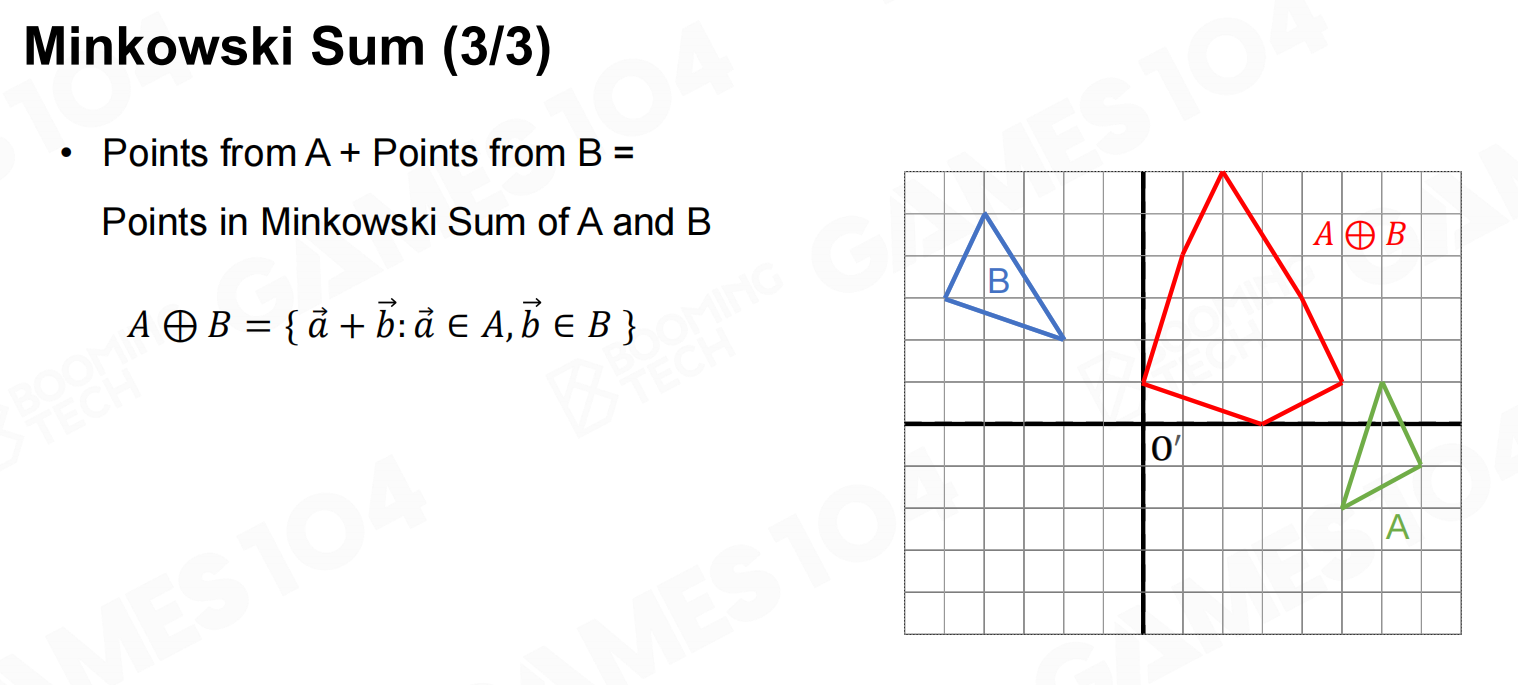
对于凸多边形,它们的Minkowski和也必为一个凸多边形,而且这个新多边形的顶点也是原始多边形顶点的和。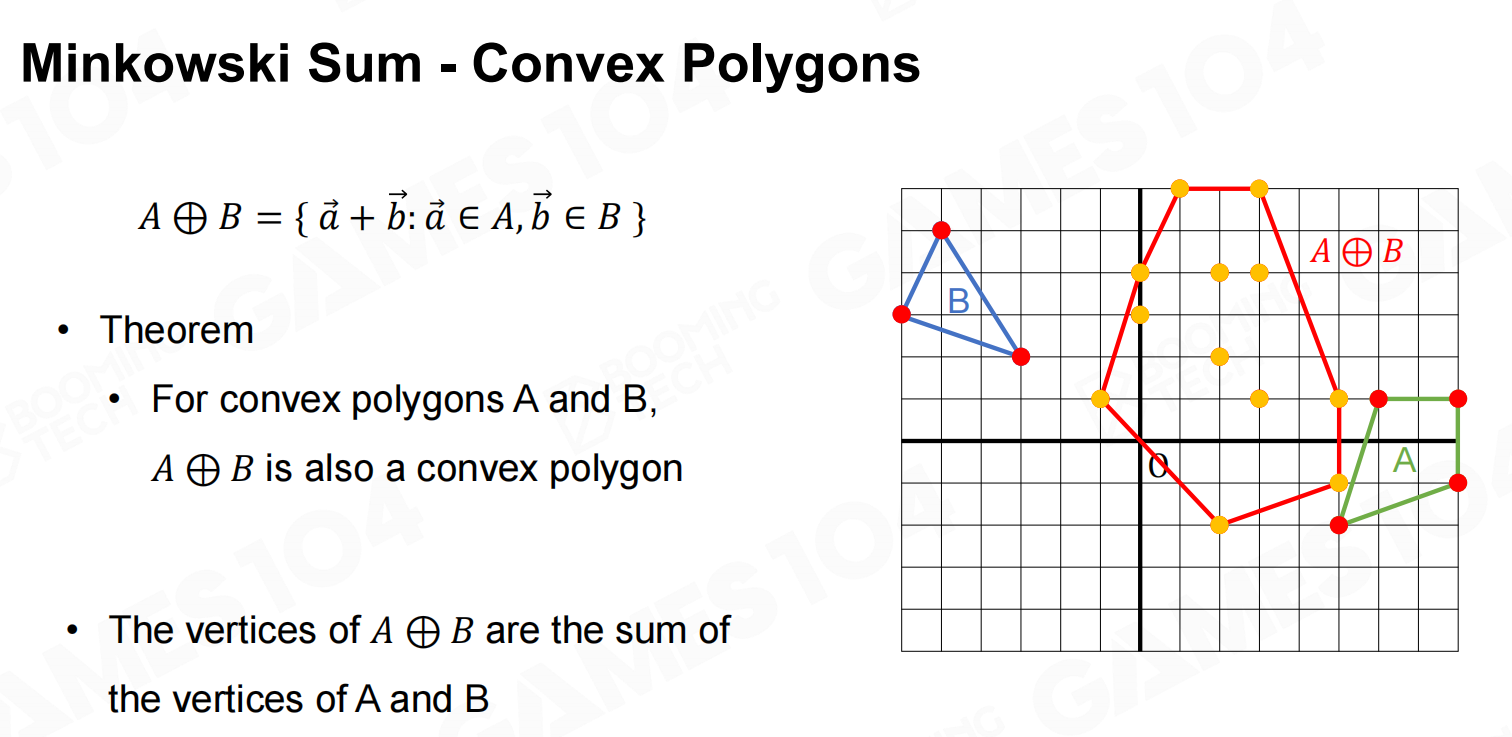
在此基础上我们定义点集
即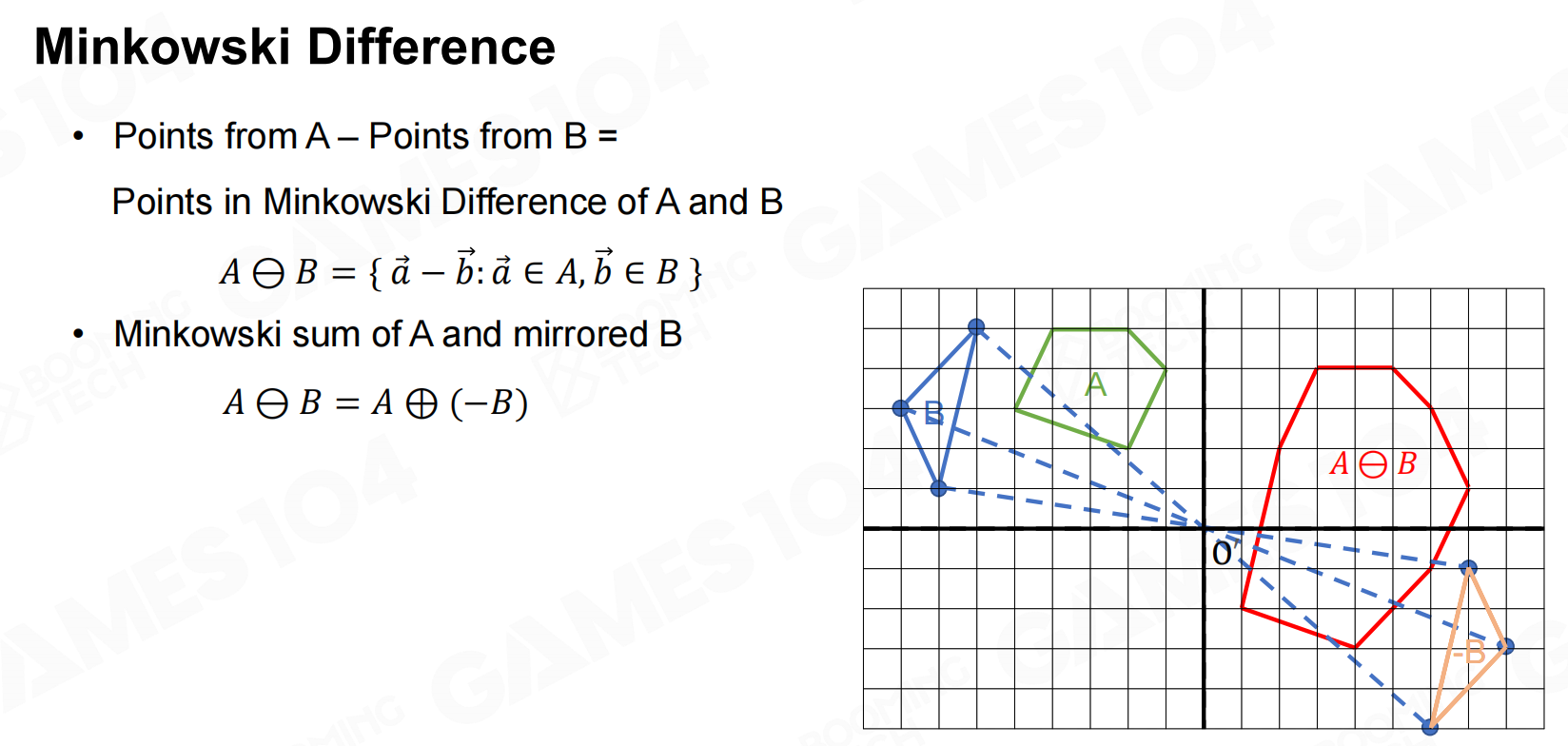
可以证明当
这样判断两个凸多边形是否相交的问题就转化为判断原点是否位于凸多边形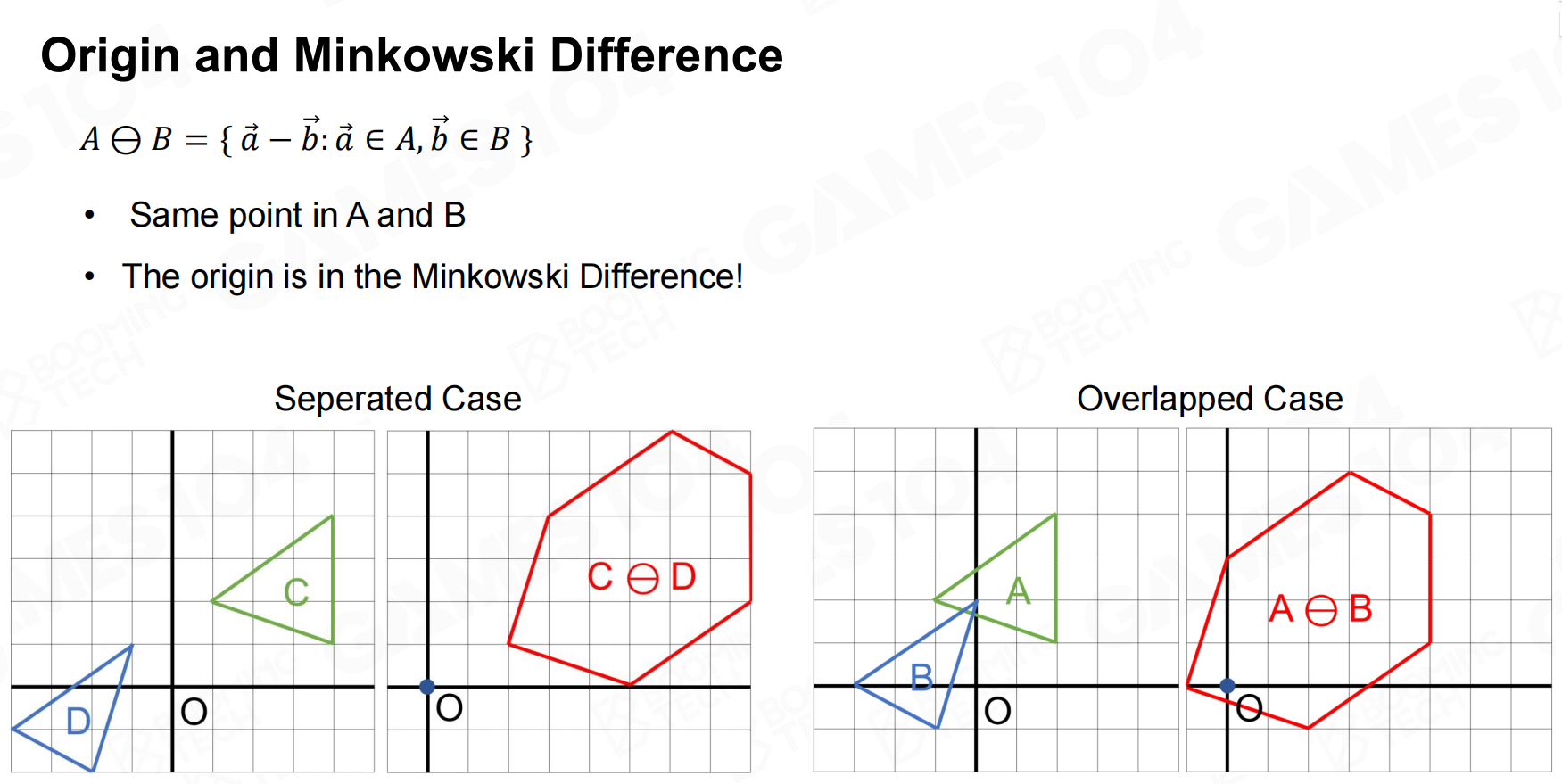
GJK算法的主要流程如下: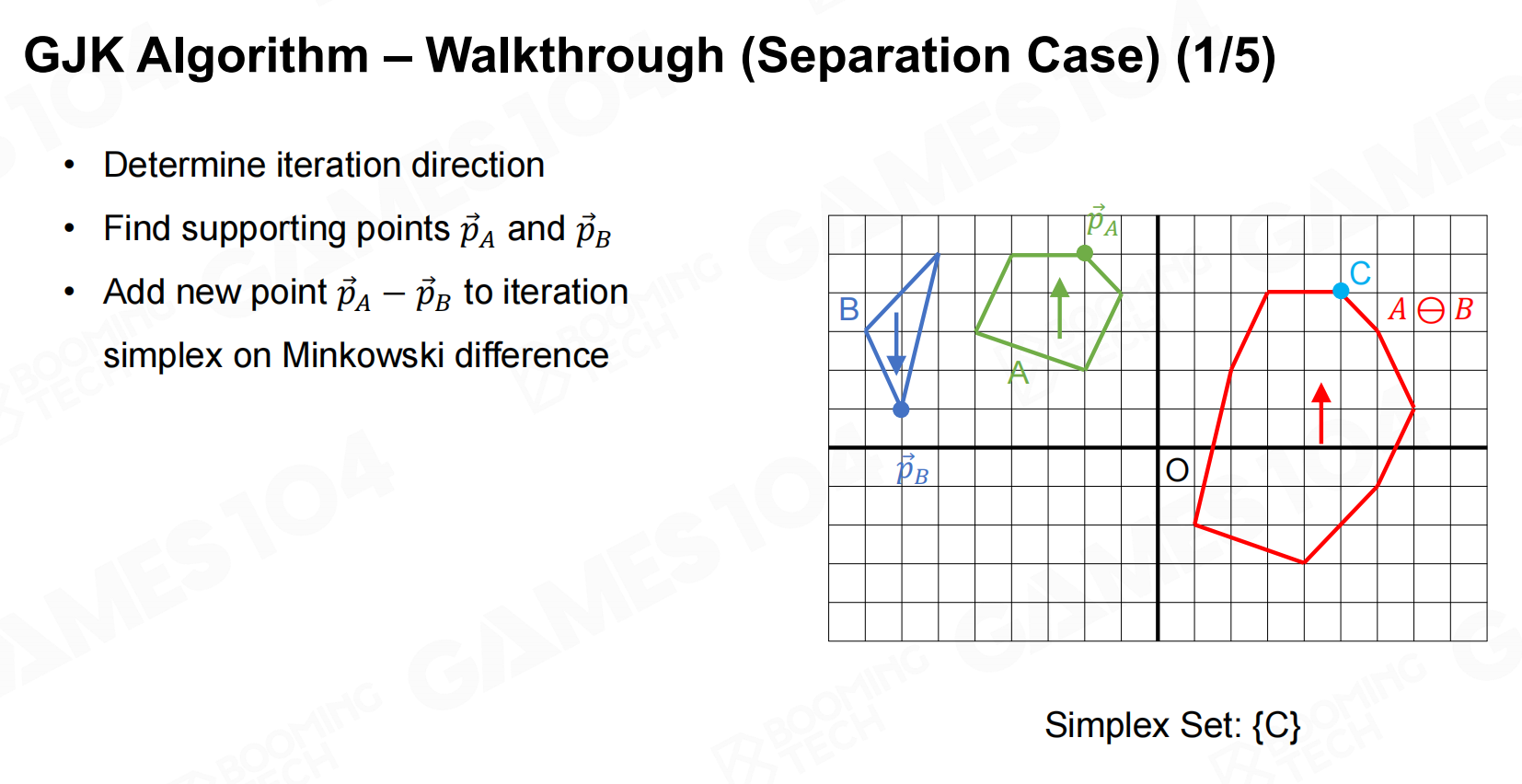

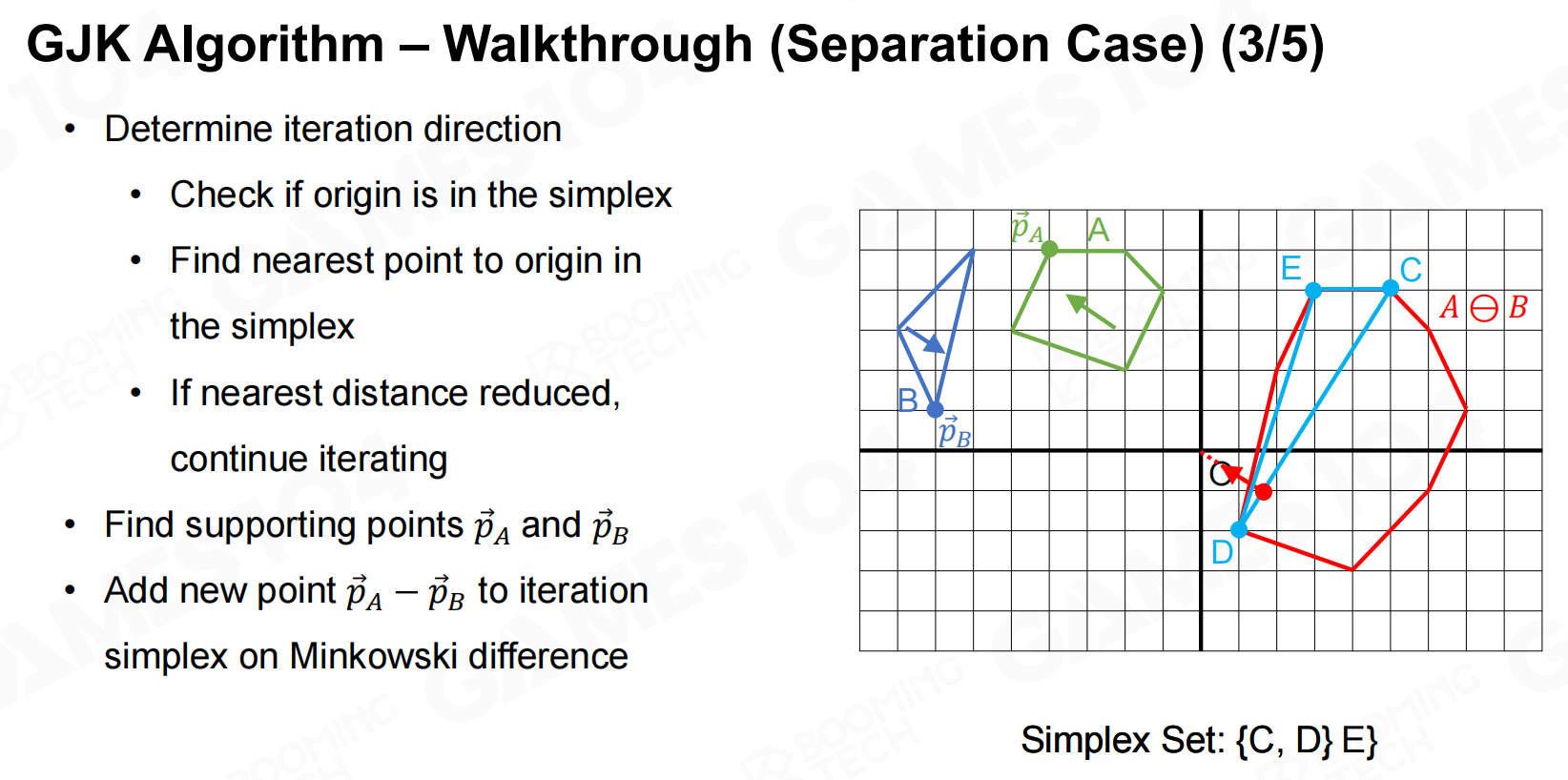
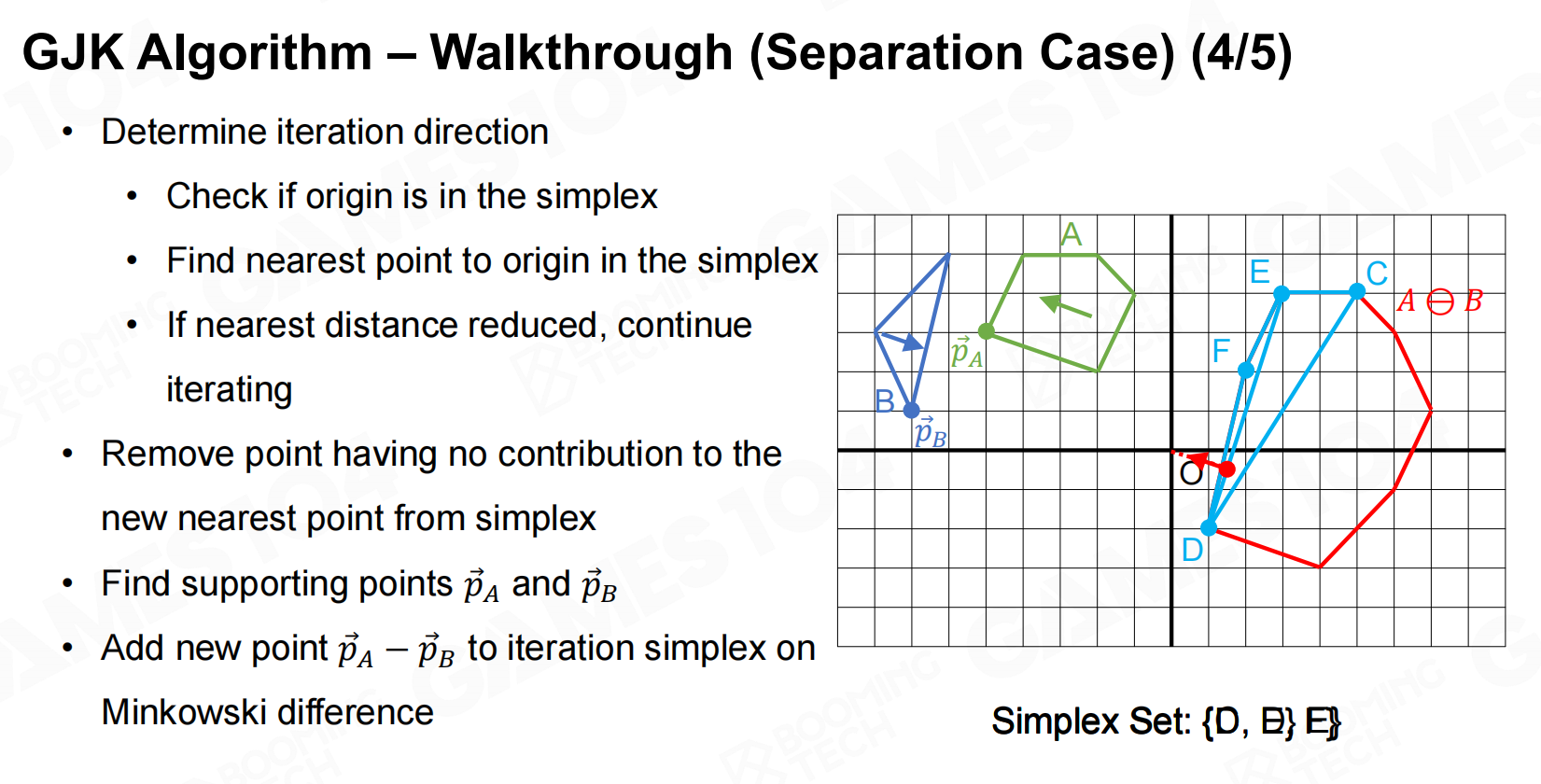
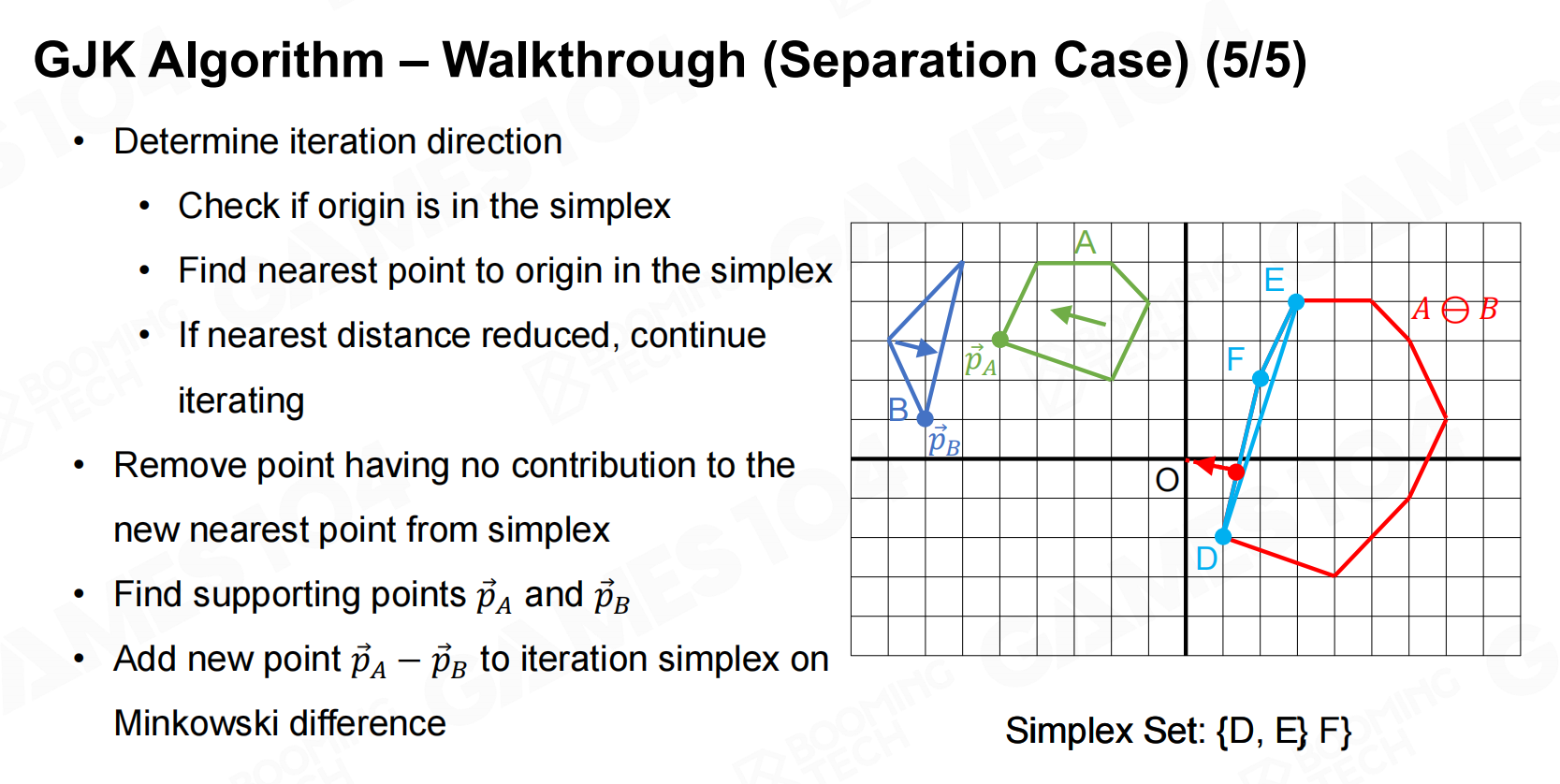
当GJK算法判断出两个凸多边形相交后还可以进一步计算交点以及深度等信息。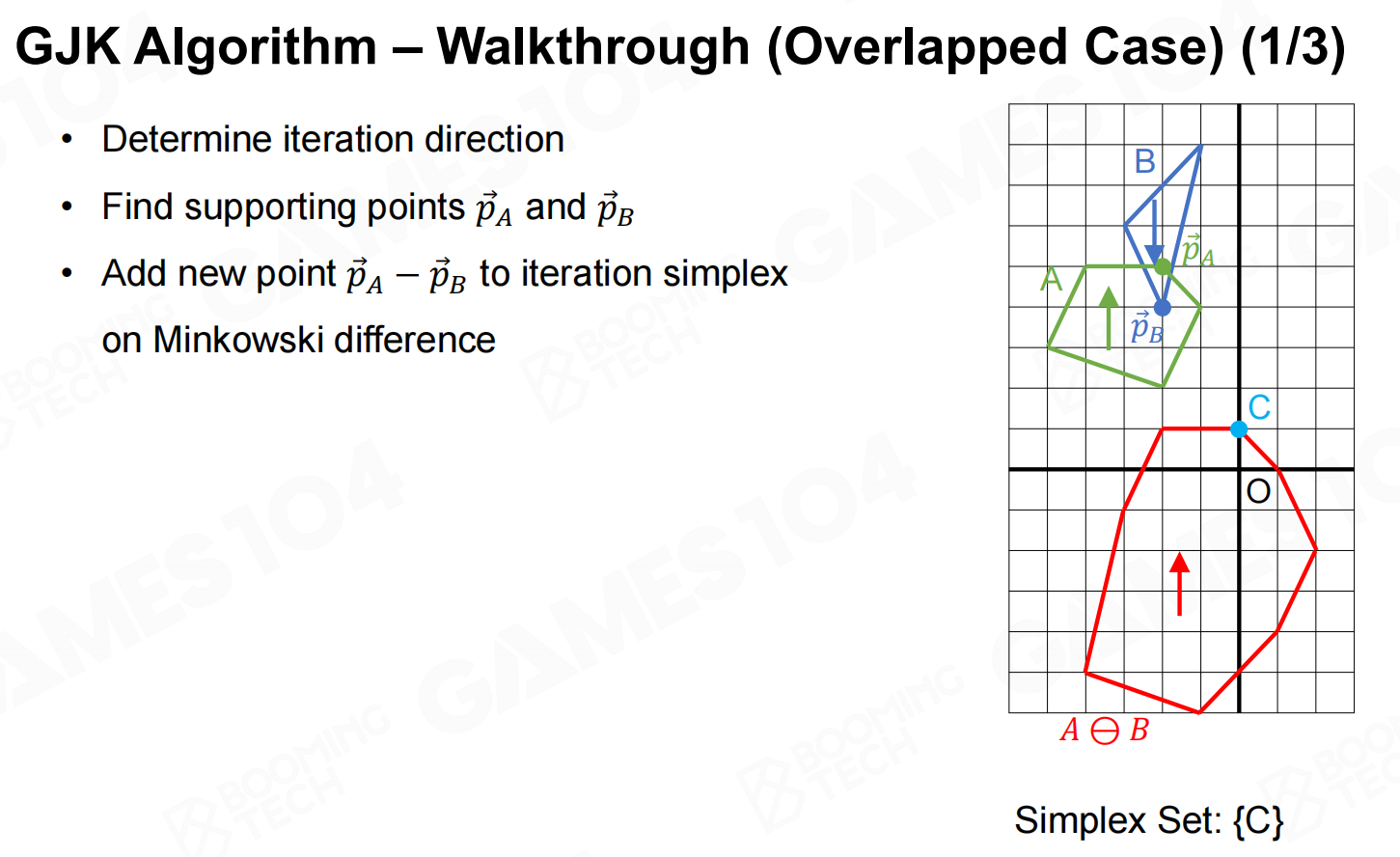

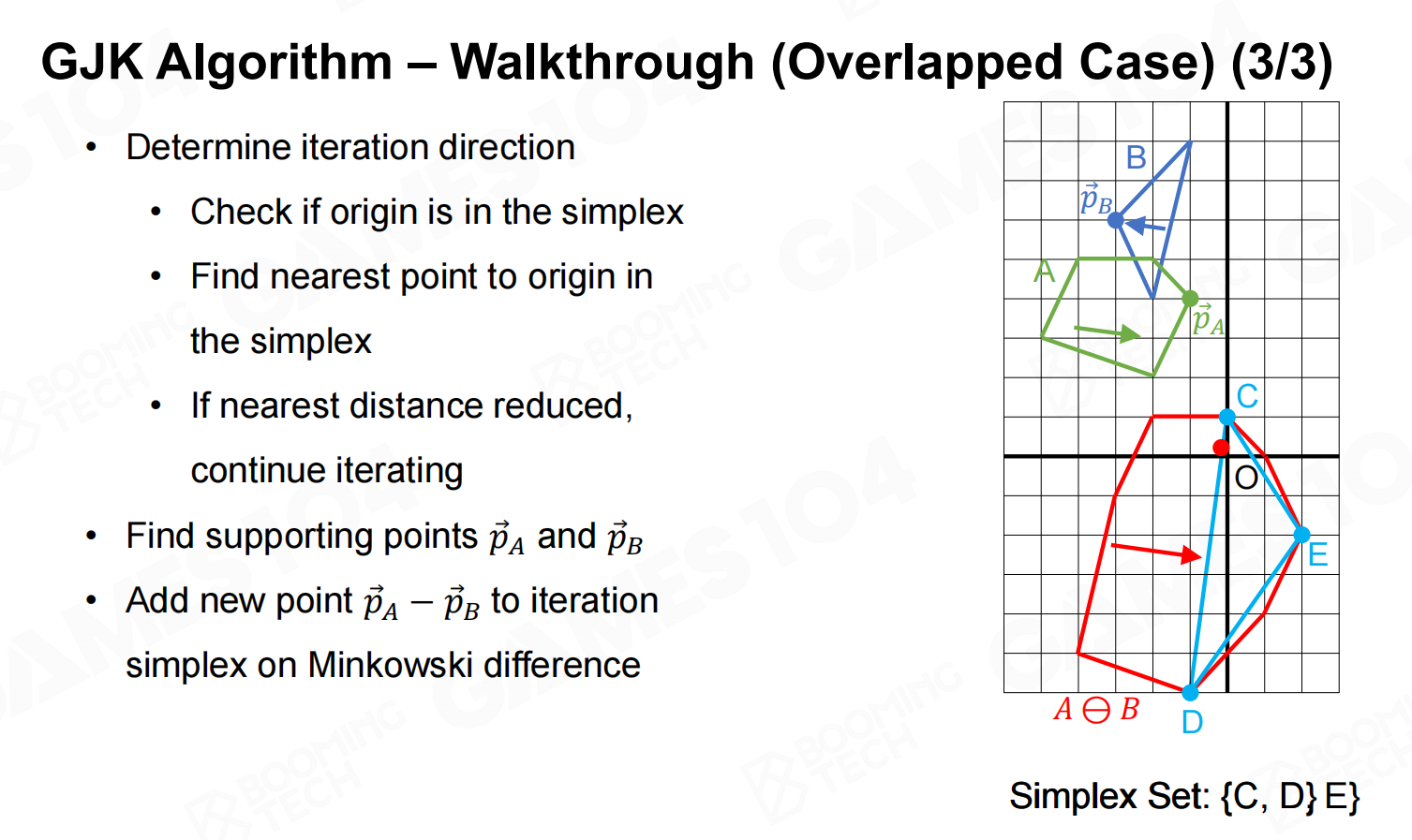
使用的方法为GJK算法。可以参考https://zhuanlan.zhihu.com/p/511164248
分离轴定理(Separating Axis Theorem)
分离轴定理(separating axis theorem, SAT)同样是一种计算凸多边形相交的算法,
它的思想是平面上任意两个互不相交的图形我们必然可以找到一条直线将它们分隔在两端。
对于凸多边形还可以进一步证明必然存在以多边形顶点定义的直线来实现这样的分隔,
因此判断凸多边形相交就等价于寻找这样的分隔直线。

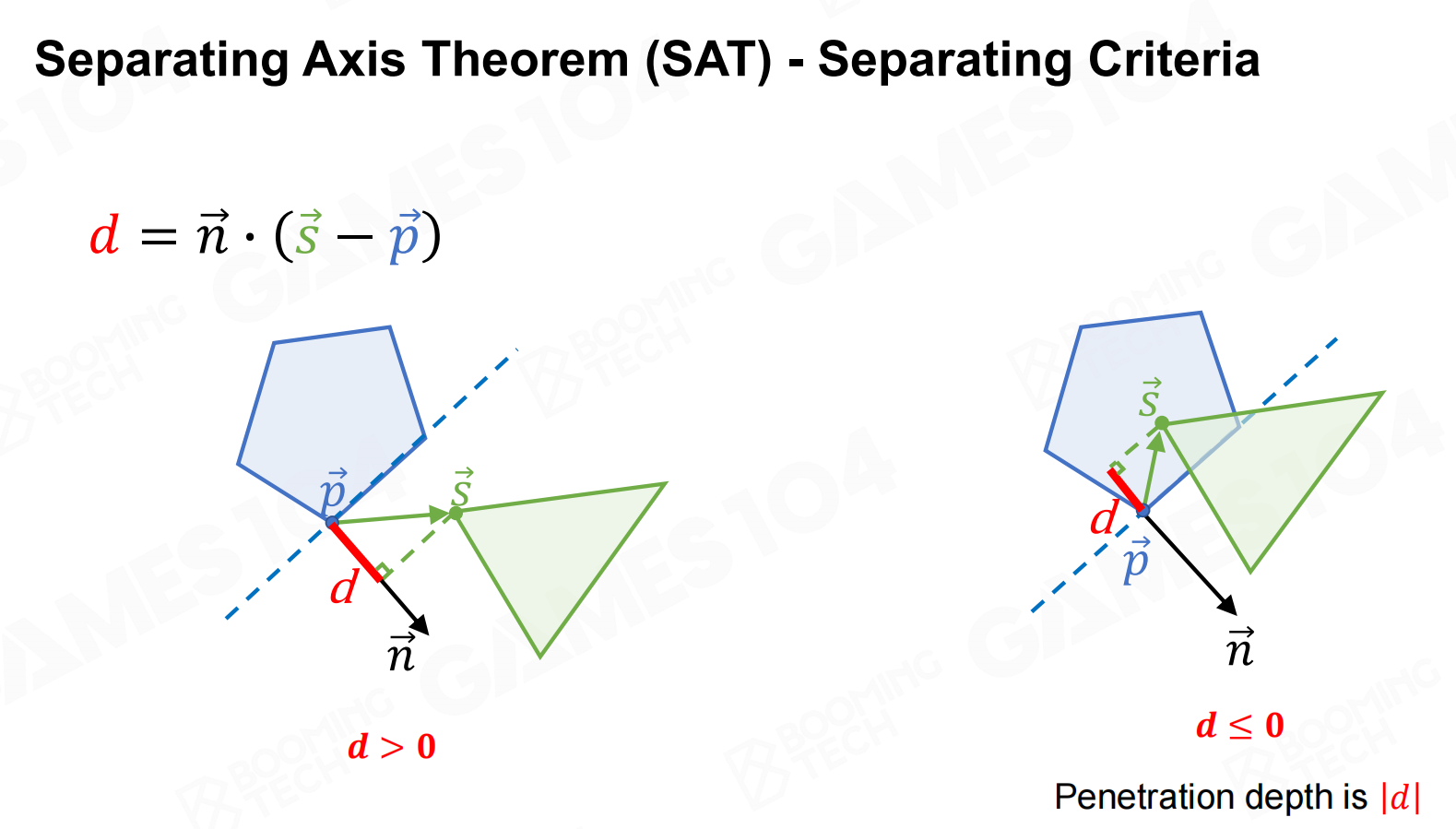
使用SAT判断凸多边形是否相交时需要分别对两个图形的边进行遍历,然后判断另一个图形上的每个顶点是否落在边的同一侧。
只要发现存在一条边可以分隔两个图形即说明它们互不相交,否则继续遍历直到用尽所有的边,此时两个图形必然是相交的。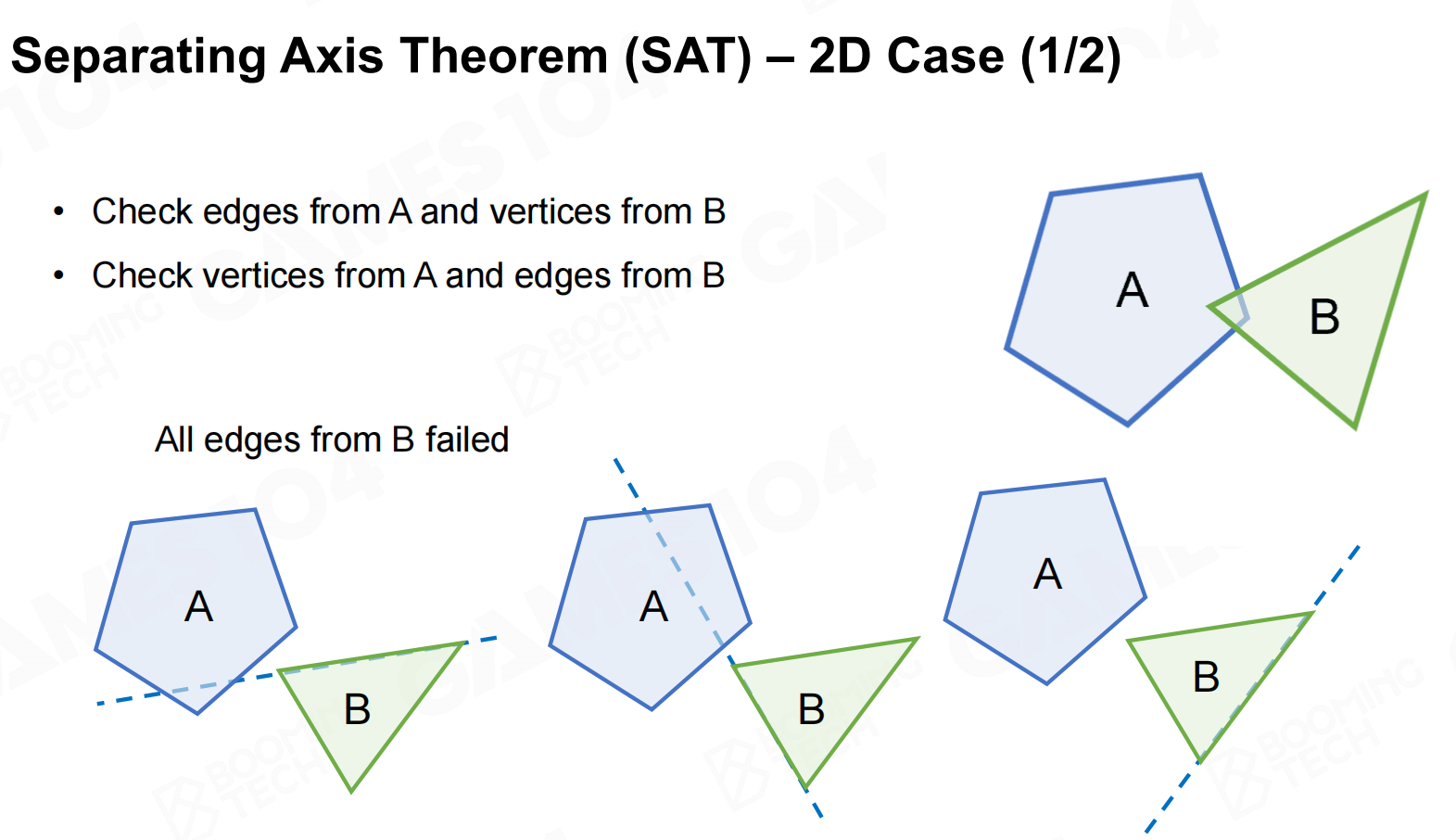
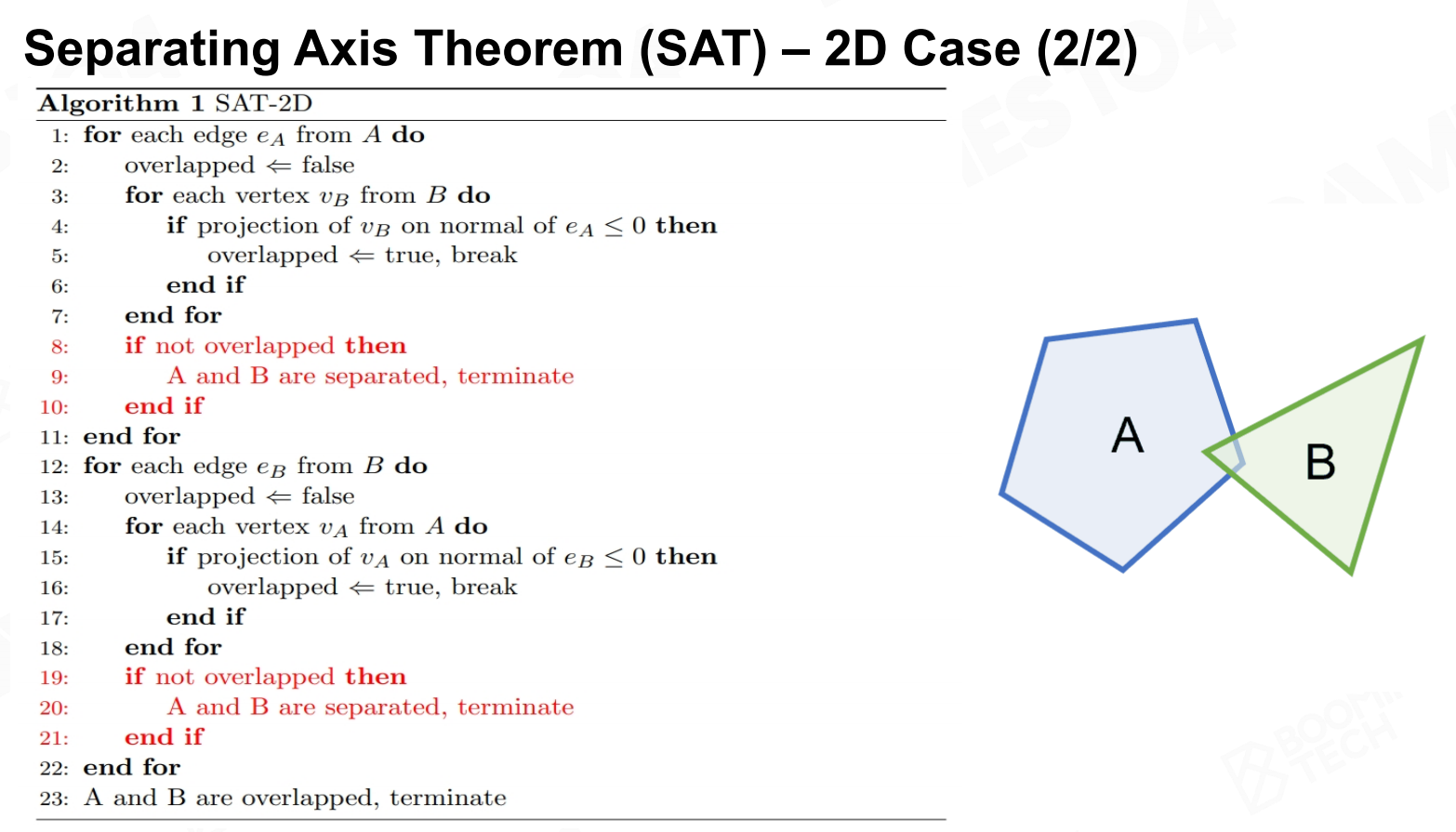
当图形的位置发生变化时还可以从上一次检测得到的分离轴开始重新进行检测,这样可以进一步提高算法的效率。
对于三维图形的情况则不仅需要考虑面和面的分隔关系,还要考虑边和边的分隔关系。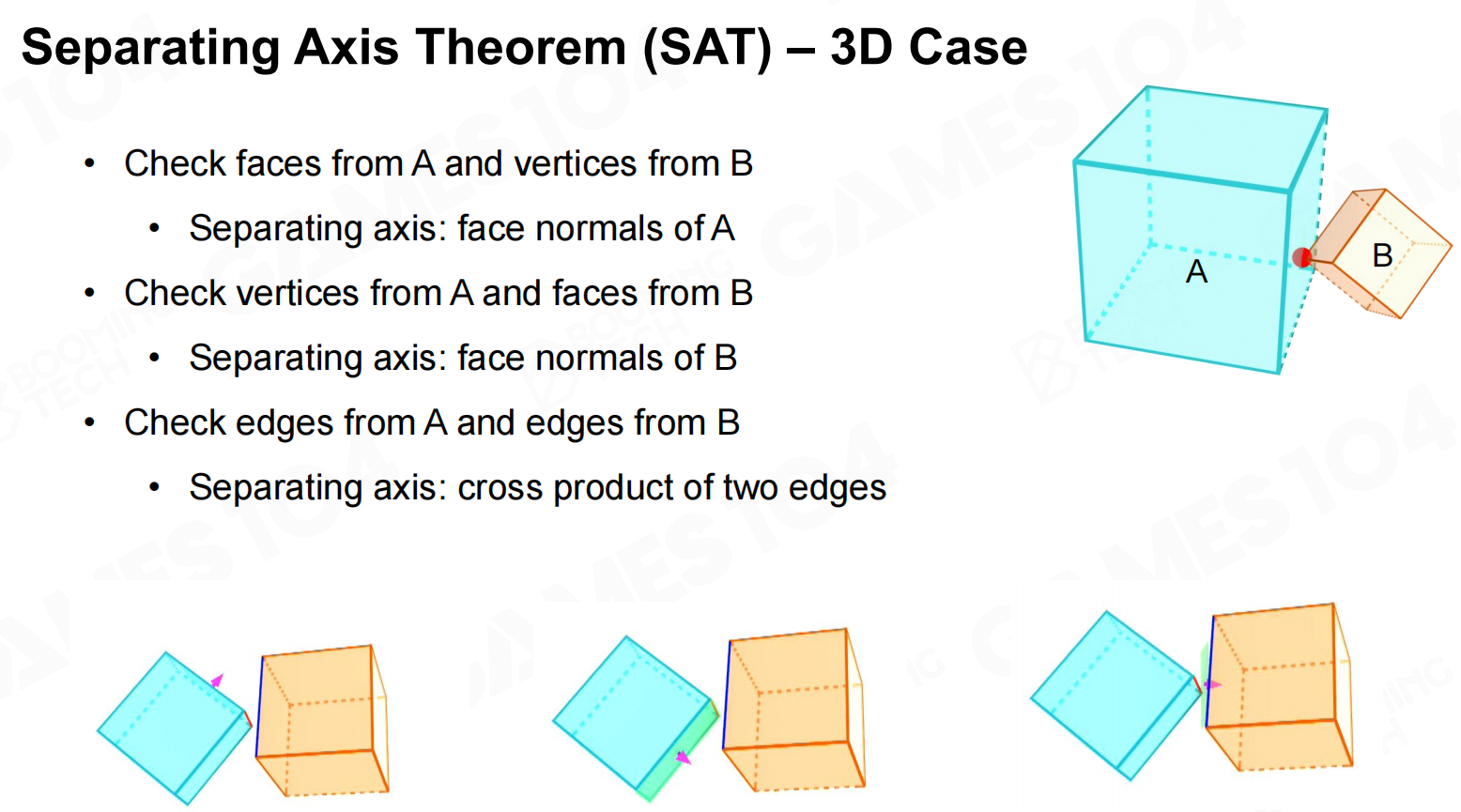
碰撞解决
完成碰撞检测后就需要对发生碰撞的刚体进行处理,使它们相互分开。目前刚体的碰撞主要有三种处理思路,
分别是penalty force、velocity constraints以及position constraints,本节课我们主要介绍前两种处理方法。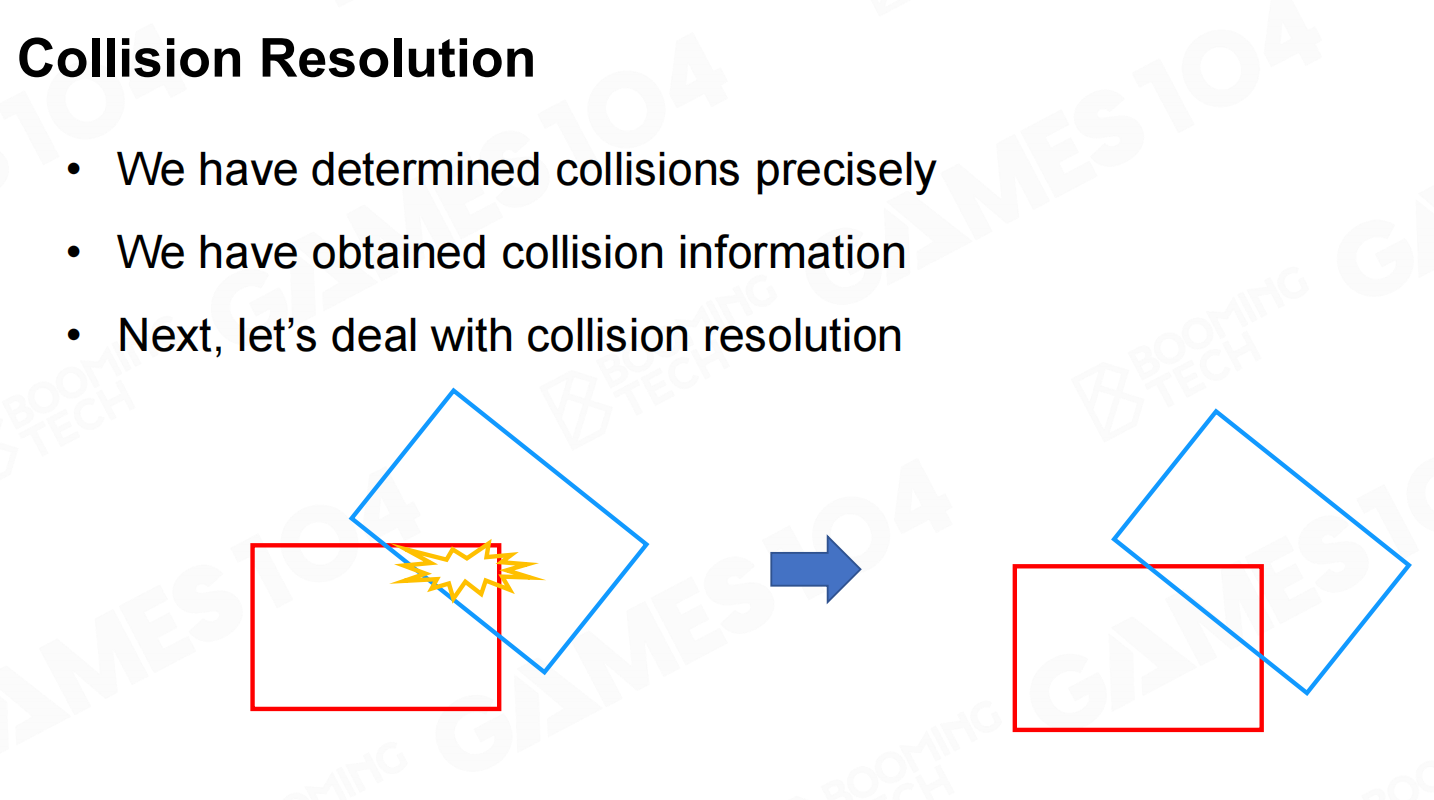

施加惩罚力(Applying Penalty Force)
Penalty force是最直观的碰撞处理方法,它的思想是当两个物体相交后沿反方向分别施加一个排斥力把它们推开。
这种方法要求设置比较大的排斥力以及很小的积分时间间隔,否则容易出现非常不符合直觉的碰撞效果,
因此现代物理引擎中几乎不会使用penalty force来处理刚体碰撞问题。
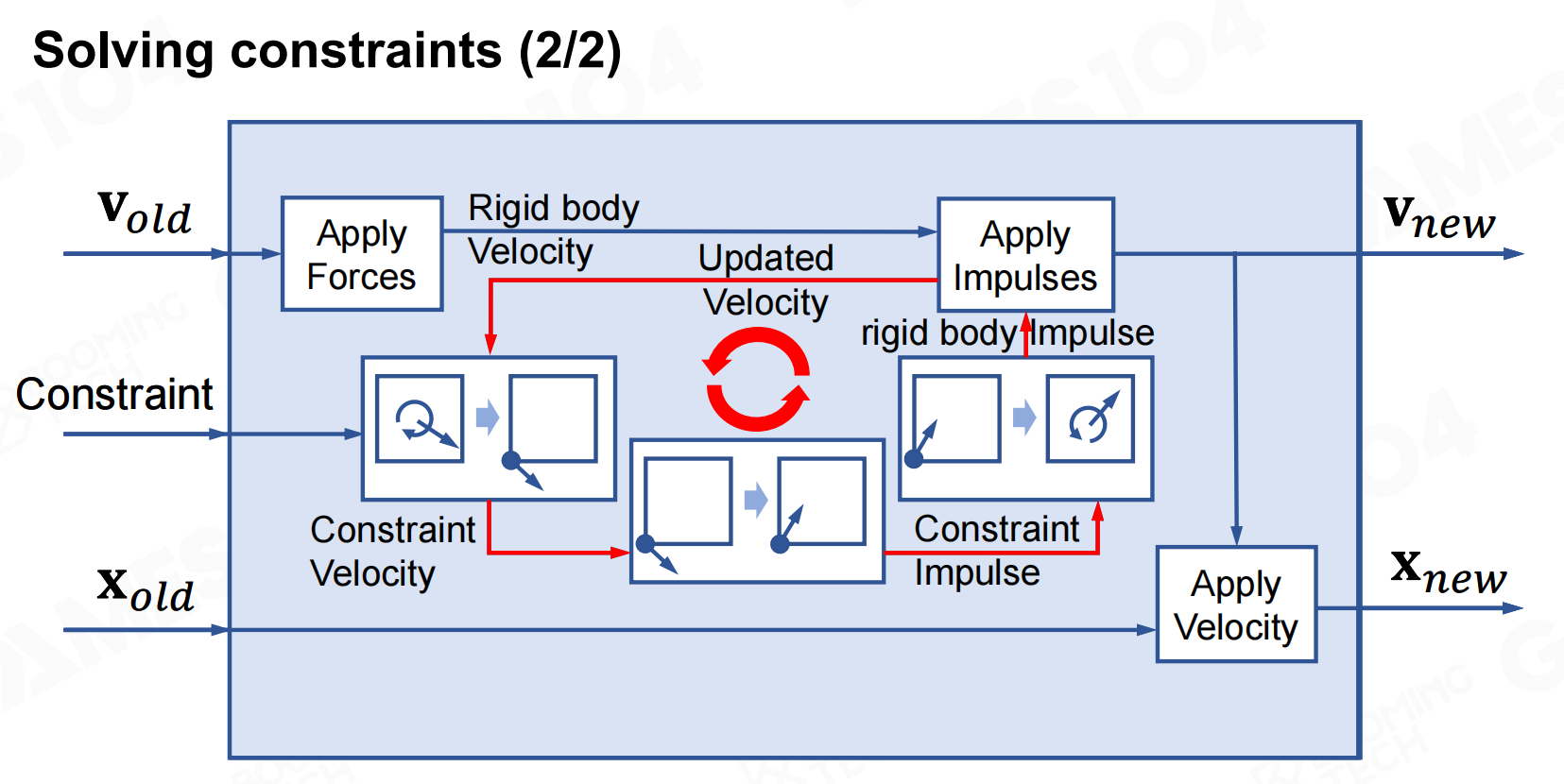
求解约束(Solving Constraints)
目前物理引擎中主流的刚体碰撞处理算法是基于Lagrangian力学的求解方法,它会把刚体之间的碰撞和接触转换为系统的约束,然后求解约束优化问题。

场景请求
除了上面介绍过的内容外,在游戏中我们往往还需要对场景中的物体进行一些查询,这些查询操作也需要物理引擎的支持。
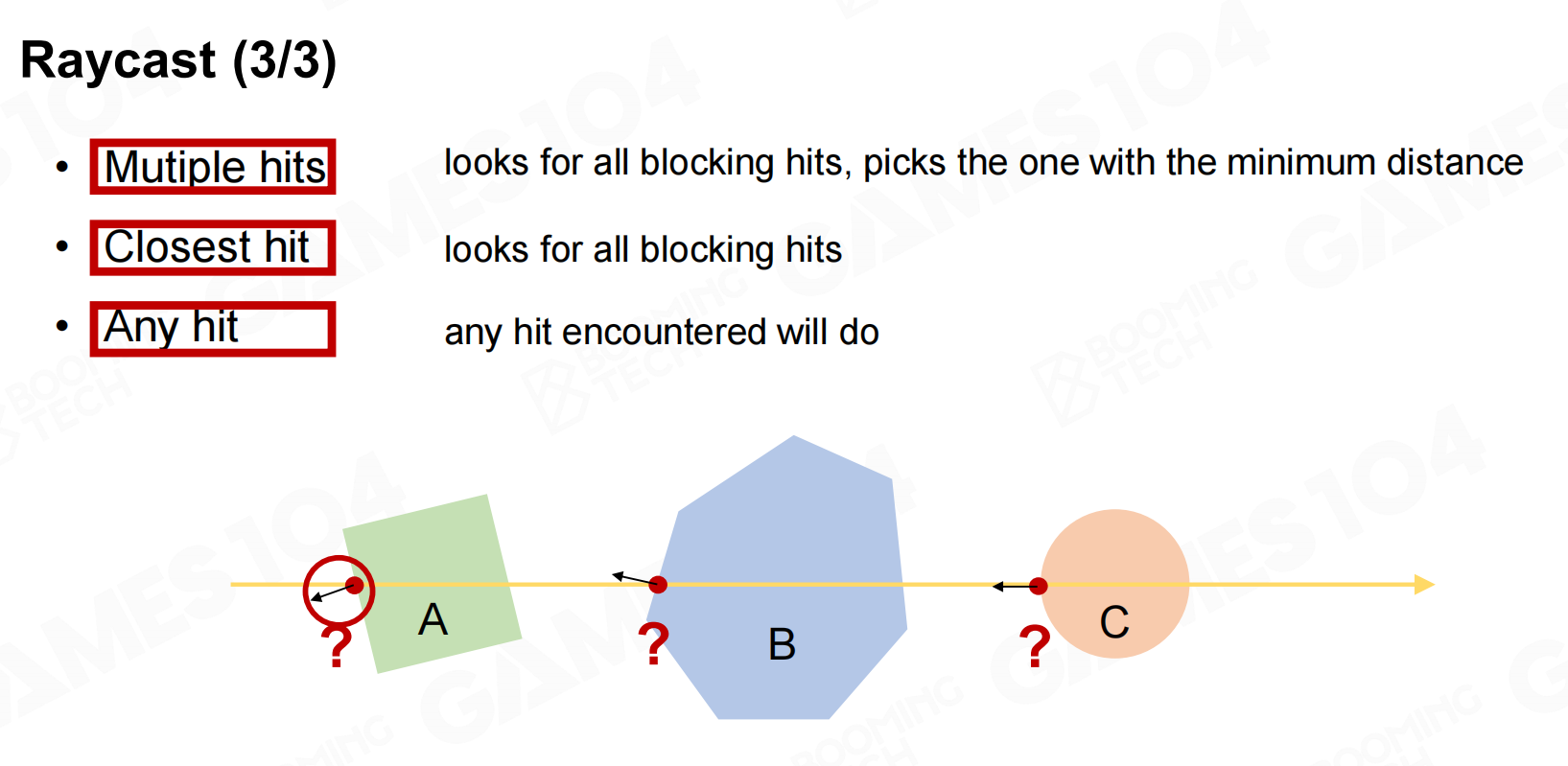
光线投射(Raycast)
Raycast是非常基本的查询操作,我们希望能够获取某条射线在场景中击中的物体。实际上在光线追踪中就大量使用了raycast的相关操作,
而在物理引擎中raycast也有大量的应用,比如说子弹击中目标就是使用raycast来实现的。

遮挡(Sweep)
Sweep与Raycast类似,不过在sweep中需要使用有一定几何形态的物体取击中场景中的其它物体

重叠(Overlap)
另一种常用的操作是overlap,此时我们需要判断场景中的物体是否位于某个几何形状中。overlap与碰撞检测非常类似,
不过overlap一般只会使用简单的几何体来进行检测。像游戏中爆炸效果的检测就是使用overlap来实现的。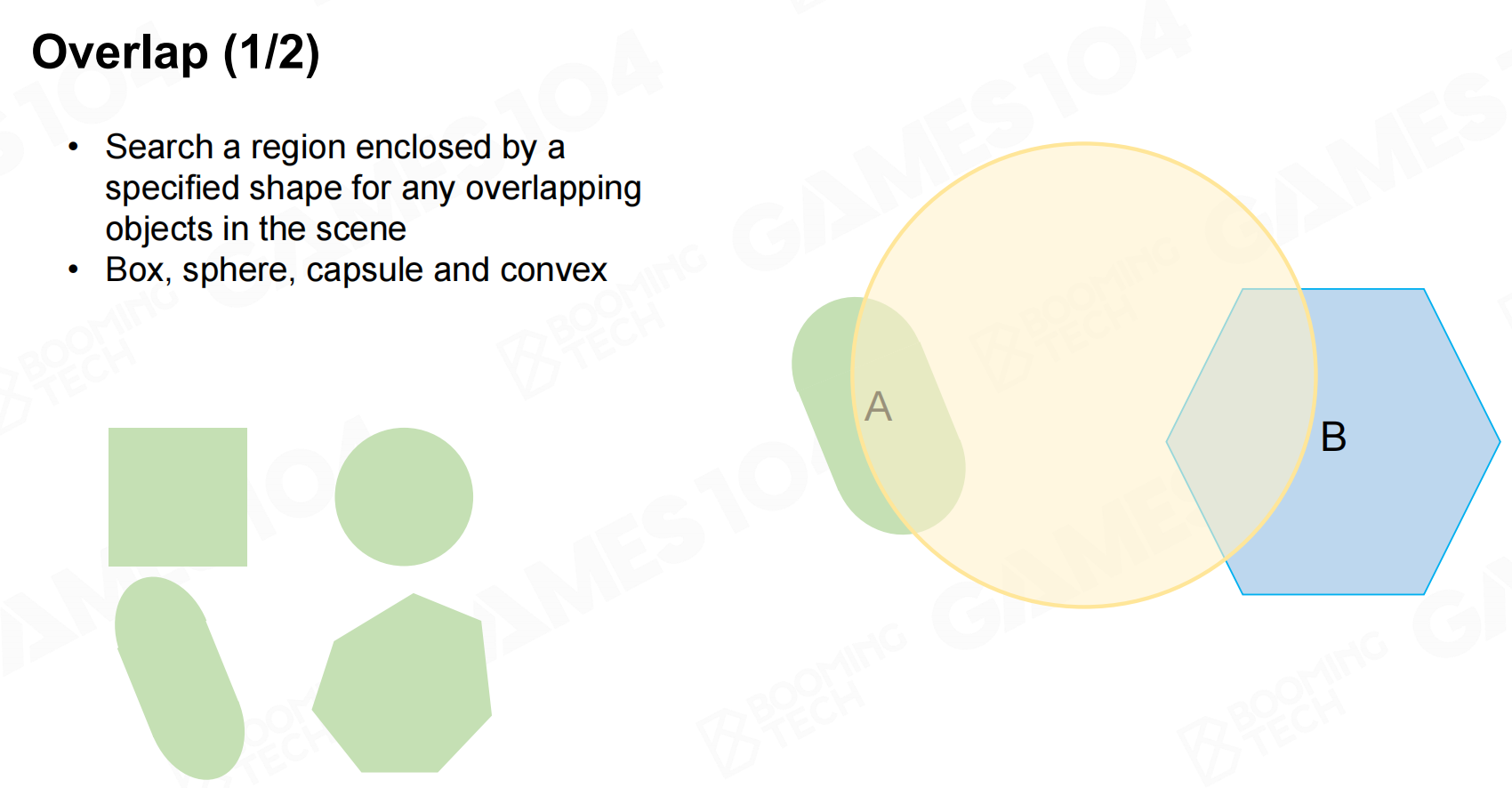

碰撞组(Collision Group)
在物理引擎中还需要额外注意对场景中的物体进行分组,这样可以提高各种物理仿真算法的效率。
效率、准确性与确定性
仿真优化(Simulation Optimization)
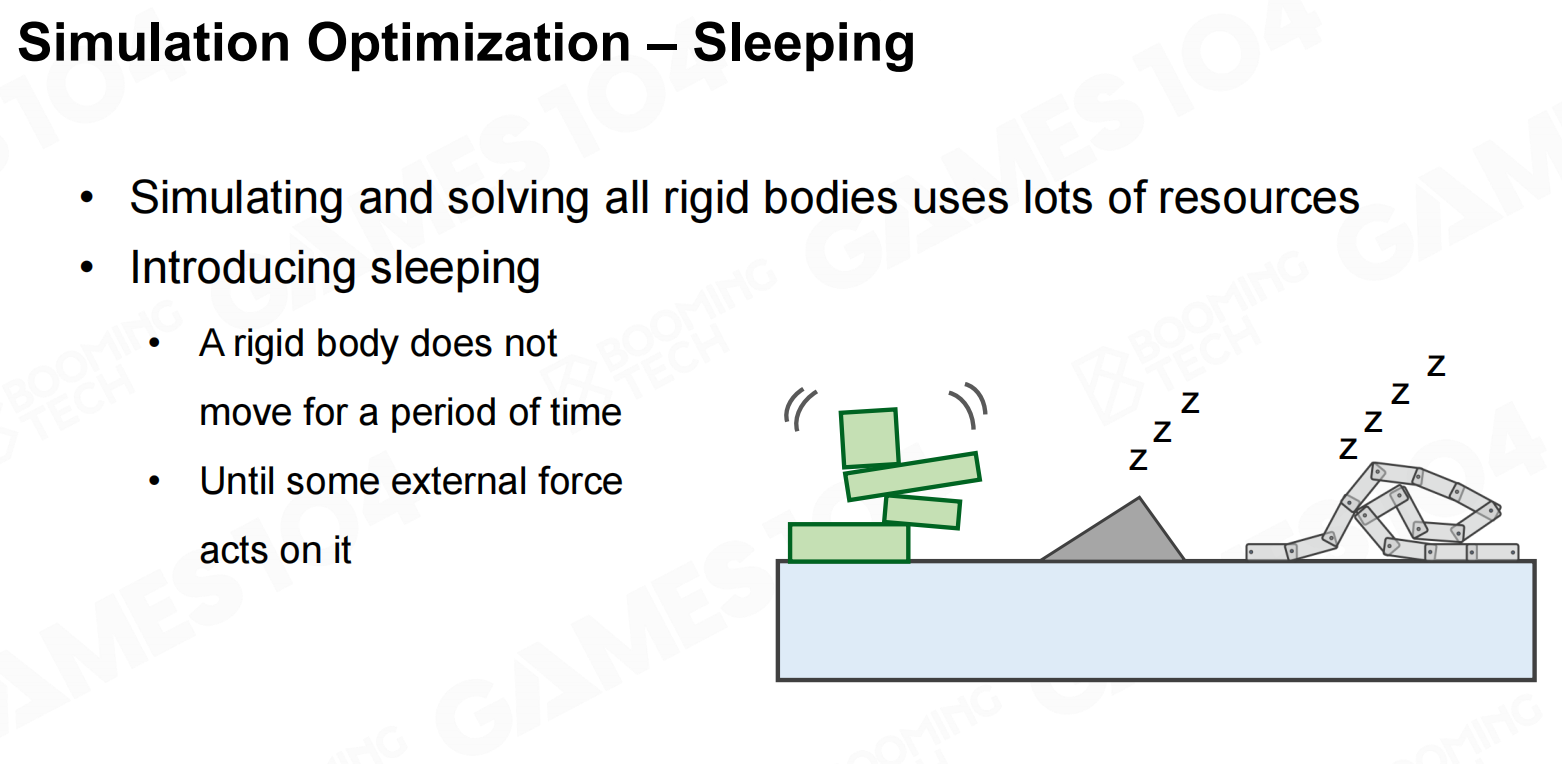
我们知道物理仿真是极其消耗计算资源的,如果在所有时刻都对场景中的物体进行模拟会造成计算资源的浪费。
因此一种常用的手段是把场景中的物体划分为若干个island,当island内没有外力作用时就对它们进行休眠,
这样就可以节约计算资源。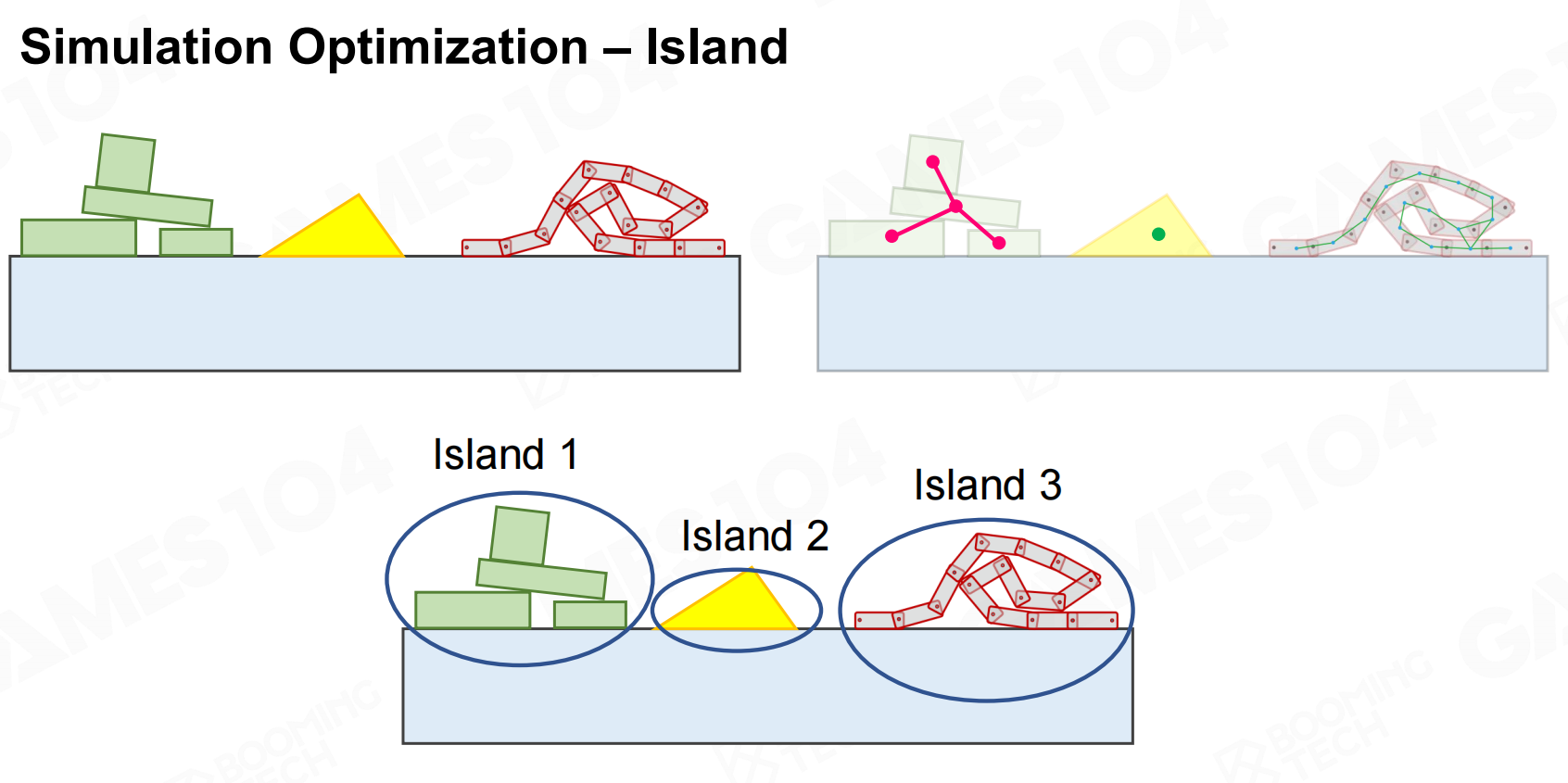
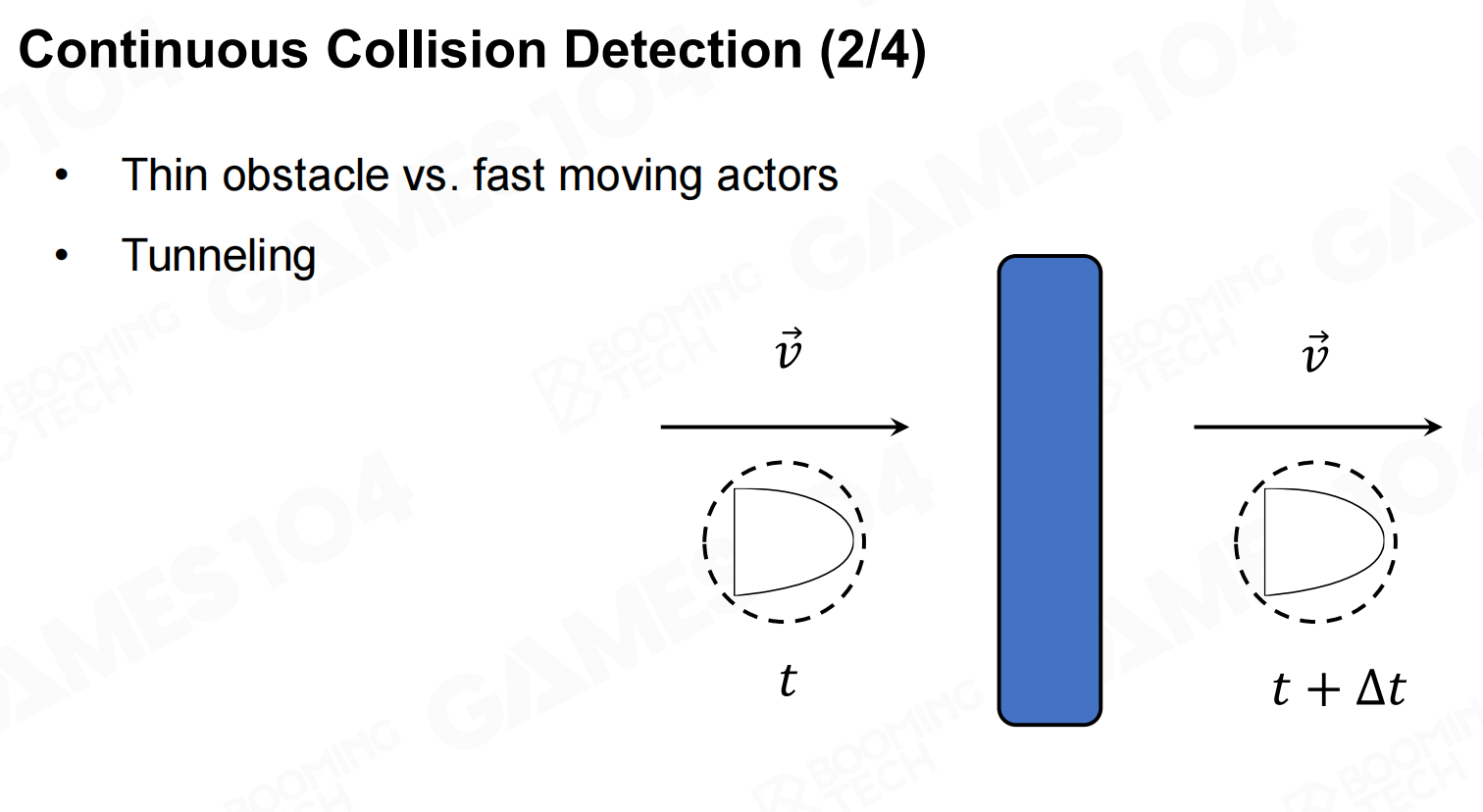
连续碰撞检测(Continuous Collision Detection - CCD)
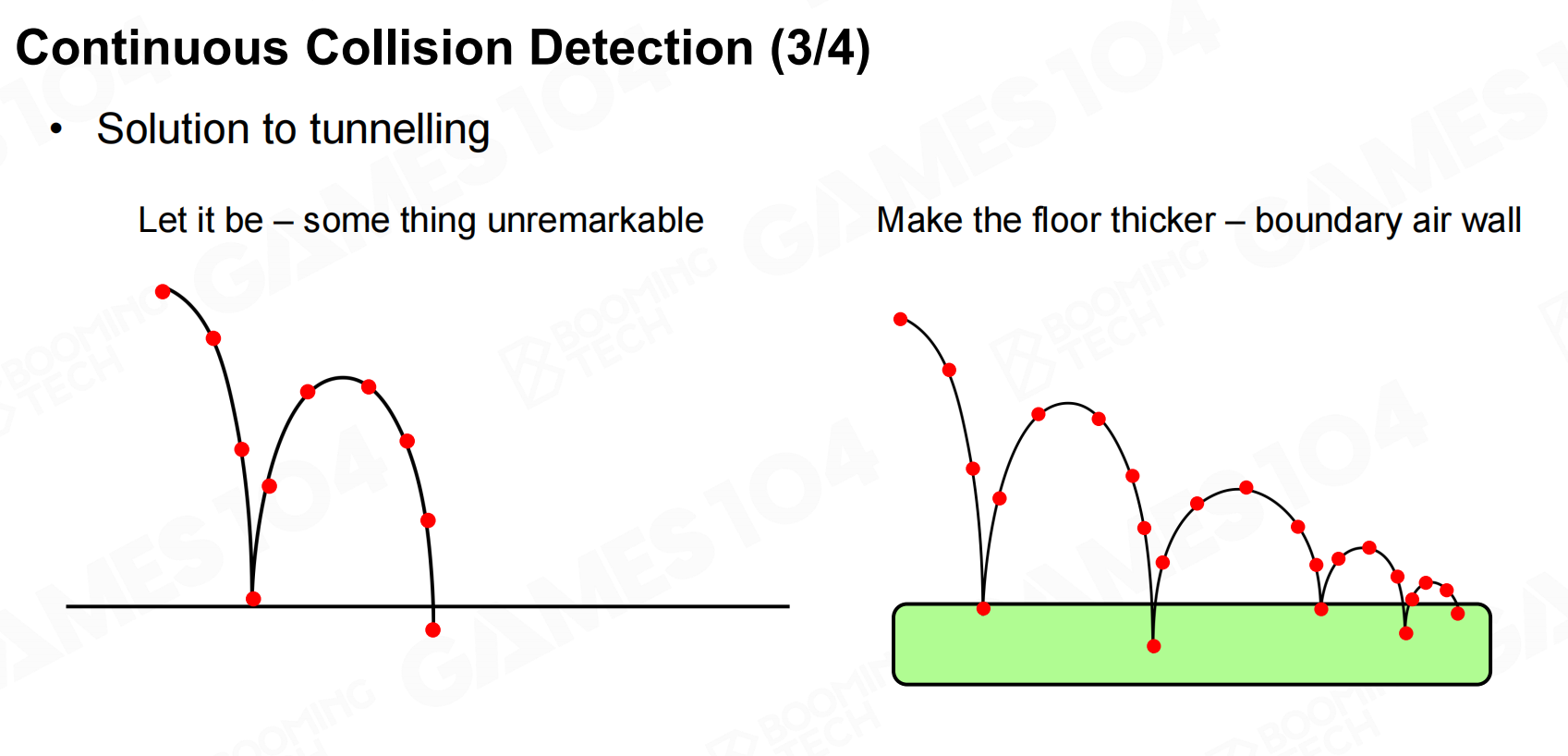
当物体运动的速度过快时可能会出现一个物体之间穿过另一个物体的现象,一种比较质朴的方法就是把墙等物体做的厚一点。
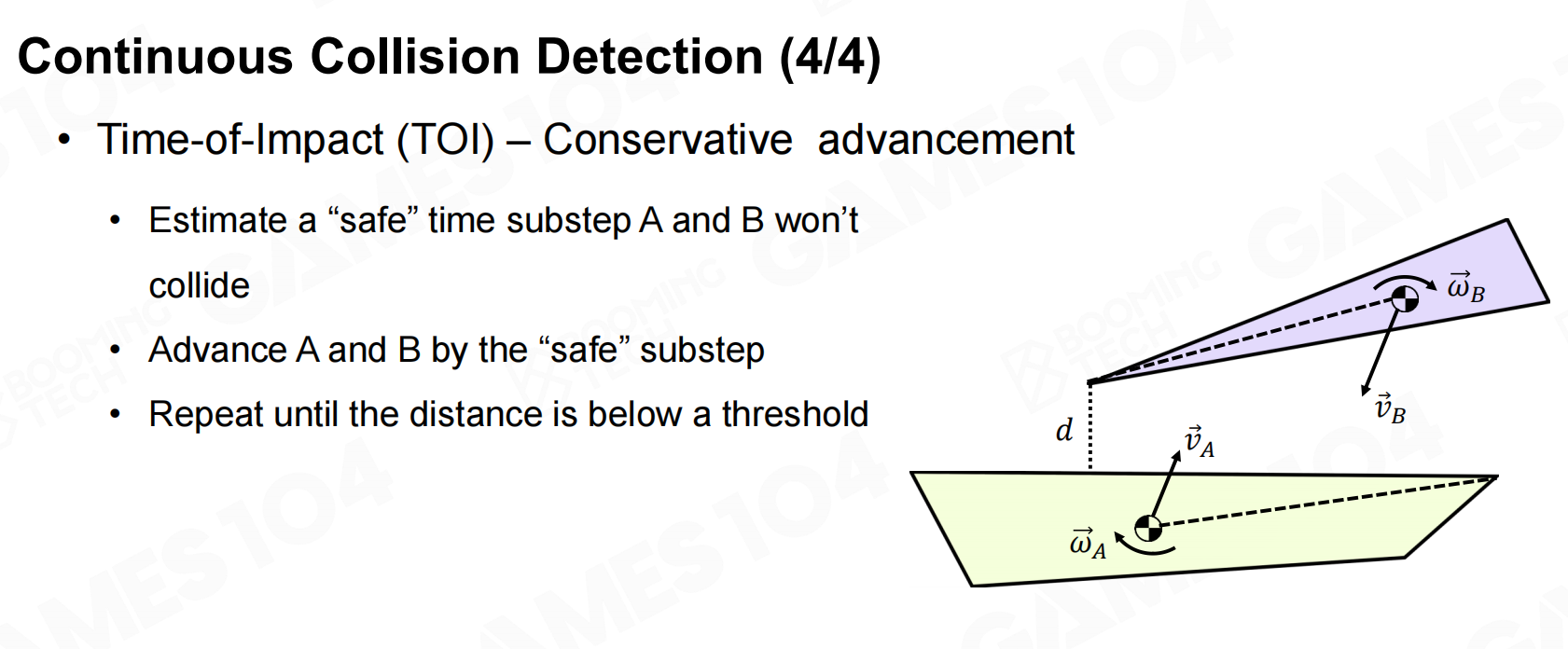
更规范的做法就是CCD:先计算一个安全时间(在这个时间内两个物体不会碰撞),然后开始一点点详细计算会不会碰撞,知道它们的距离小于一定阈值。
确定性模拟(Deterministic Simulation)
在进行物理仿真时还需要考虑仿真结果的确定性。尽管在编程时我们使用的都是同一套物理定律,
在程序运行阶段由于帧率、计算顺序以及浮点数精度等问题容易出现同一个场景在不同终端上产生不同的模拟结果。

总而言之,物理仿真仍然是比较困难的。在现代游戏引擎中还有很多开放问题待我们进行解决。
引用
- 本文作者:樱白 - Cherry White
- 本文链接:https://cherry-white.github.io/posts/de5d97c9.html
- 版权声明:本博客所有文章均采用 BY-NC-SA 许可协议,转载请注明出处!

